UFRJ- Física 3 – P2 2018.2 - DIURNO - 3
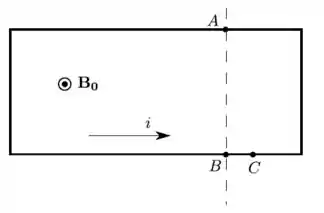
Considere uma fita retangular, feita de cobre, por onde passa uma corrente estacionária de intensidade com o sentido indicado na figura abaixo. A fita está sujeita à ação de um campo magnético constante que aponta para fora do plano da fita. Considere os pontos , e indicados na figura. Sabendo que os portadores de carga no cobre são os elétrons, podemos afirmar que os potenciais elétricos nestes pontos, dados por , e , respectivamente, satisfazem:
Passo 1
Precisamos nos lembrar que uma corrente sempre flui de um potencial mais alto para um mais baixo. Assim já podemos definir que o potencial em é maior que o potencial em .
Passo 2
Agora acontece algo interessante que nem no efeito Hall! Os portadores de carga nesse caso são elétrons que têm carga negativa. Assim o movimento dos elétrons é no sentido contrário da corrente, ou seja, para esquerda.
Pela regra da mão direita, o produto vetorial dessa velocidade com o campo aponta para cima, mas como a carga é negativa então a força sobre esses portadores aponta para baixo.
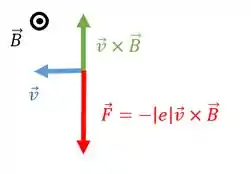
Isso faz com que haja mais cargas negativas no ponto do que no ponto o que implica que o potencial em é maior do que o potencial em , então
Juntando tudo
Resposta
Letra b.