Dois fios retilíneos, paralelos, muito longos, separados por uma distância , são percorridos por correntes estacionárias de sentidos opostos e mesma intensidade , conforme mostra a figura. Um terceiro fio, circular, de raio , é colocado entre os primeiros fios, Qual devem ser a intensidade e o sentido da corrente que esse último fio deve portar para que o campo magnético resultante no seu centro seja nulo?
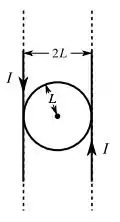
- e horário.
- e anti-horário.
- e horário.
- e anti-horário.
- e horário.
- e anti-horário.
- A corrente no fio circular deve ser zero.
Passo 1
Bem... Sabemos pela teoria que um fio reto carregando uma corrente gera campo magnético ao redor dele cuja direção é circular e o sentido é dado pela regra da mão direita. Entretanto, todavia, contudo, não obstante, o módulo desse campo pode ser dado por...
Onde é a distância do fio ao ponto que se quer calcular o campo magnético.
O campo magnético de um fio circular com uma corrente no centro pode ser dado por...
Onde é o raio da espira.
Bem, então para a solução desse problema, vamos juntar as duas coisas e ver no que dá, pode ser?
Passo 2
Primeiro vamos encontrar o campo magnético gerado do centro pelos dois fios de corrente ...
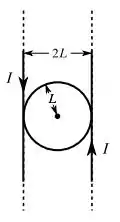
Repare que pela regra da mão direita aplicada em cima dos dois fios retos, ambos fazem um campo magnético apontados para cima no ponto do centro da espira...
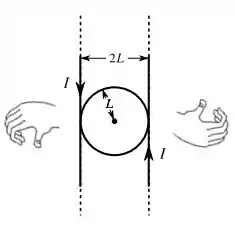
Pelo desenho não dá para ver, mas se você imaginar essas mãos direitas girando, vão perceber que dentro do circulo, os dedos apontam na direção saindo da sua telinha, logo, o campo magnético produzido no centro é a soma do campo magnético produzido pelos dois fios...
Onde é a distância do centro aos dois fios, ou seja, ...
Beleza! Então veja que se queremos zerar este campo magnético no centro, temos que ter uma corrente na espira de modo a produzir esse mesmo campo magnético, mas negativo, ou seja, entrando na sua telinha. Como podemos fazer isso?
Passo 3
Ora... Se quisermos que a corrente na espira produza um campo magnético entrando, temos que ter uma corrente girando no sentido horário...
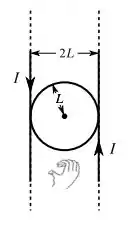
E ela tem que ter módulo igual ao módulo do campo produzido pelos dois fios no centro, ou seja...
Mas vimos no passo que o módulo do campo produzido por uma espira no centro é...
Onde é a corrente que está circulando no sentido horário na espira. Então, essa corrente em termos da corrente dos fios retos...
Resposta
Letra A.