10 - Elétrons (massa , carga ) são acelerados do repouso através de uma diferença de potencial e são então desviados por um campo magnético que é perpendicular à sua velocidade. O raio da trajetória do elétron resultante é:
- Nenhuma das anteriores.
Passo 1
Pois bem, sabemos que o elétron é acelerado do repouso e vai até uma velocidade final . Como ele sai do repouso a velocidade inicial dele é nula (). Depois disso, ele entra em um campo magnético (perpendicular à velocidade que ele atingiu ) como mostra na figura:
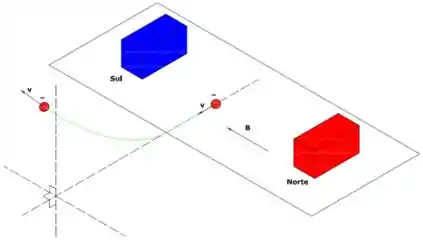
O campo magnético exerce uma força que aponta todo o tempo perpendicular a velocidade tangencial para cima, o que a faz girar com raio .
Podemos encontrar esse raio, verificando então que a força magnética atua como força centrípeta na partícula! Ora, a força magnética de um campo perpendicular à velocidade é dada por:
Já lá da mecânica, força centrípeta é:
Igualando então as duas coisas...
Agora, temos que encontrar qual é a velocidade atingida pelo elétron na aceleração! Vamos nessa?
Passo 2
Bem, sabemos que aceleração está ligada a trabalho , e o trabalho de uma carga em função da diferença de potencial é dado por:
O trabalho , também pode ser dado em função das velocidades inicial do elétron e final, de acordo com a mecânica dessa maneira aqui:
Onde é a variação da energia cinética do elétron:
Como a velocidade inicial é , então...
Isolando a velocidade em função da diferença de potencial ...
Beleza, então com essa velocidade, podemos encontrar o raio da trajetória.
Passo 3
Então...
Lembrando-se que assim como ...
Agora, lembrando que é a carga do elétron que vale :
Resposta
Letra C.