Uma espira transporta corrente em sentido horário (vista de cima da espira) está posicionada de modo que seu centro encontra-se exatamente acima do centro de outra espira que é percorrida por uma corrente em sentido oposto, isto é, em sentido anti-horário (vista de cima da espira) como mostra a figura. Em que sentido apontará a força magnética exercida sobre a espira superior?
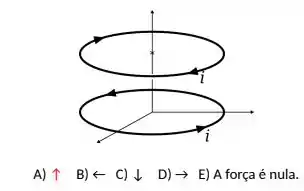
Passo 1
Bem, sabemos que a força magnética que em um fio conduzindo corrente sempre pode ser dado pelo produto vetorial...
Onde é o campo externo em cima do cabo que estamos analisando.
Então as duas grandes perguntas que temos que responder aqui é:
- Quem é o ?
- Quem é ?
Passo 2
RESPOSTA À PRIMEIRA PERGUNTA:
POW! é o vetor tangente ao cabo que estamos querendo a força. O sentido dele, vai ser sempre dado pela corrente que o cabo está transportando!
No nosso problema, o cabo onde estamos analisando a força é a espira de cima, portanto...
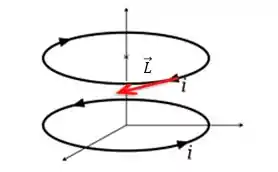
Passo 3
RESPOSTA À SEGUNDA PERGUNTA:
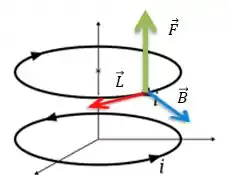
O campo , no caso, será o campo produzido pela espira de baixo em cima da espira de cima.
Pela regra da mão direita, o campo gerado pela espira de baixo na espira de cima terá a seguinte direção e sentido...
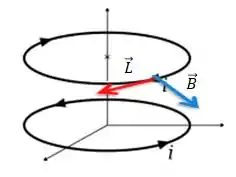
Passo 4
Bem, finalmente podemos retornar a fórmula da força magnética apresentada no passo 1:
De acordo com a álgebra, o produto vetorial de por gerará o vetor resultando que será perpendicular ao mesmo tempo ao e ao vetor . O sentido dele, é dado pela regra da mão direita saindo de e girando em sentido ao ...
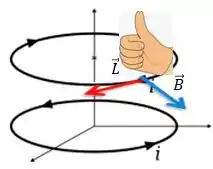
Então a força magnética na espira de cima será...
Resposta
Letra A