Um feixe de elétrons viaja a uma velocidade de . Qual deve ser a intensidade do campo magnético aplicado perpendicularmente ao feixe para que este se mova em uma trajetória circular de raio ?
Passo 1
Pow, cara! Antes de começarmos de fato o nosso problema, vamos desenhar o que está acontecendo para termos uma noção física do problema, pode ser?
Temos aqui um feixe de elétrons com uma velocidade e que vai atravessar um campo magnético perpendicular (pode ser um campo entrando ou saindo da sua telinha, mas nesse caso farei entrando):
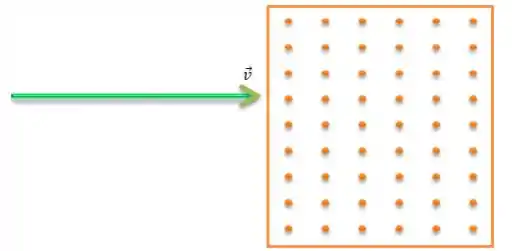
Quando o feixe entra na região, vai surgir uma força nele que é sempre perpendicular a velocidade e ao campo ao mesmo tempo em que é a força magnética (a direção dessa força vai ser para baixo pela regra da mão direita, saca?):
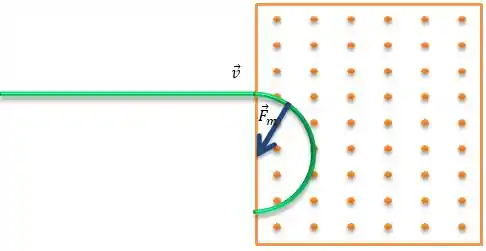
E essa força magnética, coincidentemente é uma força centrípeta, gera esse movimento circular de raio , saca?
O que queremos fazer é encontrar a intensidade do campo magnético que faz isso com esse feixe de elétrons! Bora?
Passo 2
POW! Como comentamos no passo anterior, a mágica acontece porque a força magnética é ao mesmo tempo uma força centrípeta ...
A força centrípeta pela nossa Teoria é...
E a força magnética...
No caso, deve ser a massa do elétron que está em movimento circulatório e a carga dele. Esses valores foram dados no formulário:
E a carga do elétron é...
Claro, a carga do elétron é negativa, mas aqui só nos interessa o módulo do valor por isso, pegamos a carga sendo positiva, ta ligado?
Passo 3
Bem, agora é só a gente substituir tudo na equação...
Simplificando então essa continha resolvendo então essas potências de ...
Resolvendo isso por uma calculadora...
Que é o mesmo que...
Resposta
Letra D.