A figura abaixo ilustra diferentes partículas sendo injetadas por uma abertura no ponto em uma região com um campo magnético uniforme perpendicular à velocidade das partículas, que é a mesma para todas as partículas. O campo é perpendicular à página e aponta para “fora” dela. As patículas descrevem as trajetórias identificadas por I, II, III e IV.
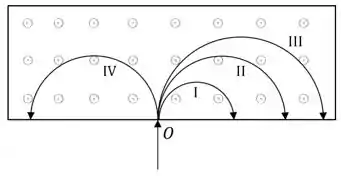
Quais das afirmativas a seguir são verdadeiras?
1. A partícula da trajetória II possui carga negativa e a da trajetória IV possui carga positiva.
2. Supondo que todas as partículas tenham mesma carga, a da trajetória II tem maior massa que a da trajetória I.
3. Supondo que todas as patículas tenham mesma massa, a da trajetória III tem maior carga que a da trajetória II.
4. Se o módulo do campo magnético B fosse aumentado, todas as trajetórias teriam um raio menor.
a) 2 e 4
b) 1, 3 e 4
c) 1, 2 e 3
d) 1 e 2
e) 3 e 4
Passo 1
Essa questão fala sobre cargas se movendo em campos magnéticos.
Sempre que uma carga , se movendo com velocidade , entra em um campo magnético , ela vai estar sujeita a essa força aqui:
É esse produto vetorial aí que vai determinar a direção da força magnética.
Vamos ver o que acontece com as cargas positivas e negativas quando entram nesse campo.
Passo 2
Todas as cargas começam com uma velocidade apontando na vertical para cima quando passam pela abertura .
E o campo magnético aponta para fora da página em todos os pontos dessa região.
Então vamos usar a regra da mão direita para ver o que isso nos diz:
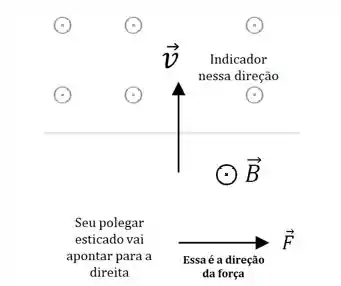
Mas cuidado! Essa é a força que age sobre as cargas positivas.
Quando a carga é negativa (), o sinal da força também é trocado, e então ela vai apontar para a esquerda.
Olhando o desenho do enunciado, isso já diz que as cargas I, II e III são positivas, e a carga IV é negativa.
Com isso a gente já pode descartar a afirmativa 1.
Passo 3
Tá, já discutimos o sinal das cargas. Mas o enunciado também faz algumas afirmações sobre o raio e a massa das partículas.
Como a gente pode descobrir isso? É só lembrar que essa força magnética está agindo como uma força centrípeta!
Já que os vetores e são sempre perpendiculares, o módulo desse produto vetorial é:
Então, tirando o módulo dos dois lados da equação:
E pela segunda lei de Newton essa força é
Nesse caso, é a aceleração centrípeta , então:
Dividindo por dos dois lados:
Ok, já conseguimos uma expressão que envolve o raio da trajetória e a massa da partícula.
Passo 4
A afirmação 2 diz que, se as cargas são iguais, a partícula II tem maior massa que a partícula I.
Vamos dar uma olhada na equação de cima:
Ou seja, quanto maior a massa da partícula, maior é o raio da sua trajetória.
A partícula II tem raio maior que a partícula I, ou seja, se a carga das duas é a mesma, então a massa da partícula II também deve ser maior.
A afirmativa 2 está correta.
Passo 5
A afirmação 3 diz que, se as massas são iguais, a partícula III tem carga maior que a partícula II.
Vamos voltar à equação de cima:
Então, quando maior é a carga, menor é o raio da trajetória.
A partícula III tem raio maior do que a partícula II, então a sua carga deve ser menor.
A afirmativa 3 está errada.
Passo 6
Por último, a afirmativa 4 diz que se o campo magnético tivesse seu módulo aumentado, todas as trajetórias teriam um raio menor.
Pela mesma equação de antes:
O raio da trajetória é inversamente proporcional ao módulo do campo!
Ou seja, quando o módulo do campo aumenta, o raio das trajetórias realmente diminui.
A afirmativa 4 está correta. Ou seja, ficamos com a letra (a).
Resposta
Letra (a).