USP, Sem Campus, Física 3, Listas de Física 3 - USP - Lista 1 - Lei de Coulomb, Campo Elétrico, Lei de Gauss, Questão 4b
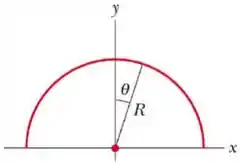
4) A figura ao lado mostra um fio não condutor carregado, em forma de semicírculo. Obtenha o vetor campo elétrico no centro, admitindo: (b) que a densidade de carga varia segundo , onde é constante.
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nessa questão temos um fio não condutor carregado e nosso objetivo é obter o vetor campo elétrico no centro do semicírculo gerado pelo fio de densidade de carga .
E aí, perece complicado né? 👀
Para obter o campo elétrico de uma distribuição de cargas, temos que aplicar a fórmula diferencial do campo elétrico
Preparado? Bora começar! 😊
Passo 2
No nosso caso, tanto , quanto é constante, ou seja
Porém, como a componente do campo elétrico que nos interessa é apenas a componente já que o fio possui uma simetria no eixo .
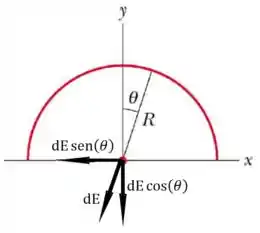
Assim, a equação deve ser adaptada como
Mas a quantidade de carga presente em uma linha infinitesimal do fio é dada pelo produto da densidade de cargas com uma variação infinitesimal do comprimento do fio, ou seja
O comprimento do fio é dado pelo comprimento de arco , ou seja
E por último, como a densidade de carga , temos
Tranquilo até aqui? Até agora apenas montamos a equação do campo 😱
Passo 3
Por fim, substituindo na equação de , temos
Integrando nos dois lados, vamos obter
Como o fio é contido entre e , então temos que aplicar esses valores ao limite de integração
Simplificando...
Como ...
Estamos quase acabando! 😁
Passo 4
Temos que escrever o resultado em função de , então se
Como já vimos que , então
Integrando nos dois lados...
Aplicando os mesmos limites de integração...
Portanto...
Substituindo em , finalmente vamos obter
Sacou como faz? Responde Aí! 😉
