UFRJ – Física 3 – P2 – 2019.2 – Questão 2
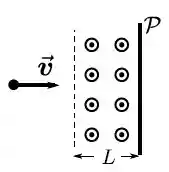
A figura mostra um campo magnético constante (uniforme e estacionário) preenchendo uma faixa retangular de altura muito grande e largura . Se uma partícula de massa e carga elétrica , com velocidade , incidir perpendicularmente a tal faixa, qual o módulo máximo que sua velocidade pode ter para que ela não colida com o painel ?
Passo 1
Se liga! Aqui a ideia é que quando uma partícula carregada em movimento entra em um ambiente onde existe a presença de um campo magnético, ela será curvada pela força magnética.
Como a velocidade é perpendicular ao campo, temos que
Passo 2
Um outro ponto a ressaltar é que a curva feita pela partícula se assemelha ao movimento circular. Sendo assim, podemos dizer que existirá uma resultante centrípeta
Passo 3
Para que a partícula não colida com o painel, ela deve ser curvada para sair em uma direção paralela a do painel, sendo assim, o raio da sua trajetória deve ser . Como a partícula pode sair por cima ou por baixo, podemos nos preocupar apenas com o módulo.
Igualando a força magnética com a resultante centrípeta, temos
Portanto, a alternativa correta é a letra (a).