A figura mostra um íon de massa e carga que é acelerado, a partir do repouso, pela aplicação de uma diferença de potencial entre sua posição inicial e o orifício que existe na placa metálica superior.
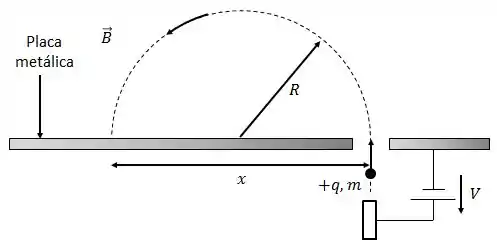
Na região acima desta placa é aplicado um campo magnético de intensidade , uniforme e perpendicular à folha. Este campo faz a trajetória do íon descrever um semicírculo, indo atingir a placa a uma distância .
Em termos de , , e , calcule:
- A velocidade do íon ao travessar o orifício da placa;
- A distância entre o ponto em que o íon passa no orifício e o ponto em que ele colide com a placa;
- Qual o sentido do vetor ? Justifique, fazendo representação vetorial na figura;
Passo 1
- A velocidade do íon ao travessar o orifício da placa;
- A distância entre o ponto em que o íon passa no orifício e o ponto em que ele colide com a placa;
- Qual o sentido do vetor ? Justifique, fazendo representação vetorial na figura;
Quando o íon é acelerado, toda a energia potencial transmitida para ele se torna energia cinética. Assim, podemos dizer que:
Passo 2
Assim que o íon entra na região com o campo magnético, esse realiza uma força magnética sobre o íon, que passa a descrever um movimento circular.
A distância corresponde ao diâmetro da trajetória circular,
Assim, a força magnética sobre o íon deve ser igual à força centrípeta que o mantém nessa trajetória circular. Logo:
Agora, podemos substituir o valor que encontramos para a velocidade:
Passo 3
O sentido do campo magnético deve ser tal que a força magnética mantenha o íon na trajetória circular.
A força magnética sobre uma carga em movimento é dada por:
Assim, pela regra da mão direita, vemos que o campo magnético deve apontar “para dentro da página” para que a força magnética mantenha o íon na trajetória circular.
Resposta
a.
b.
c.
O campo magnético aponta para dentro da página.