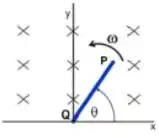
A figura mostra uma pequena barra condutora , contida no plano , que tem sua extremidade pivotada ao eixo , de forma a poder girar livremente em torno dele com velocidade angular de módulo constante . Um campo magnético constante (estacionário e uniforme), perpendicular ao plano de seu movimento e orientado no sentido negativo do eixo , ocupa o semi-espaço superior , como mostrado na figura. Sabendo que no instante inicial , qual dos gráficos abaixo melhor representa a diferença de potencial , como função do tempo, a cada volta completa em torno do eixo?
Escolha uma:
. 
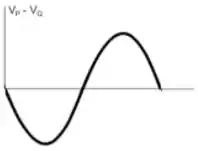
. 
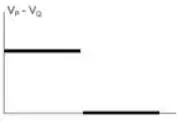
. 
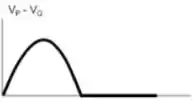
. 
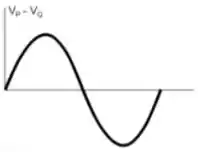
. 
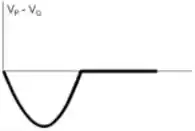
. 
Passo 1
Vem comigo que a gente resolve essa juntos!
Para sabermos o comportamento da diferença de potencial na barra, vamos usar a força de Lorentz para entender o que acontece nessa barra.
Mas para considerarmos essa força, temos que ter carga em movimento e onde está essa carga? Então, como a barra é condutora ela tem elétrons livres em sua composição, logo quando ela se movimenta teremos esses elétrons em movimento também.
Então a força de Lorentz vai agir sobre esses elétrons fazendo eles serem deslocados para uma das extremidades da barra.
Com isso teremos um acúmulo de cargas positivas em uma das extremidades e acúmulo de cargas negativas na outra, então teremos um potencial positivo em uma extremidade e um potencial negativo na outa extremidade.
Passo 2
Vamos então ver para onde os elétrons se deslocam, temos:
Essa força só vai agir onde temos campo magnético, então onde o campo for zero, não temos força e com isso os elétrons não vão ser mais deslocados logo a diferença vai ser nula.
A barra realiza um movimento circular, então os elétrons têm um vetor velocidade tangente a trajetória deles. Esse vetor muda com o tempo, mas o campo não.
Passo 3
Se fizermos o produto vetorial entre e em qual ponto dentro do campo teremos uma força apontando para o ponto , mas temos que lembrar que os elétrons têm carga negativa.
Então temos que inverter o sentido da força por conta desse sinal, então ela vai apontar para o ponto .
Então os elétrons serão deslocados para o ponto , então teremos um potencial negativo em e um positivo em , então quando fazemos:
Teremos um valor negativo.
Resumindo nossa situação, a diferença de potencial em vai ser constante e negativa e para a diferença vai ser nula, logo o gráfico que comina com o que temos é o da letra .
Resposta
. 