USP, Sem Campus, Física 3, Listas de Física 3 - USP - Lista 1 - Lei de Coulomb, Campo Elétrico, Lei de Gauss, Questão 3
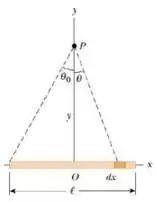
3) Um fio isolante uniformemente carregado tem comprimento e densidade de carga uniforme , como mostrado na figura ao lado. O ponto se situa à distância do fio, verticalmente sobre seu centro. (a) Mostre que o campo elétrico em é dado por
Dica: Explore a relação e integre sobre a variável angular.
(b) Obtenha o campo elétrico para do fio infinito, , a partir do resultado do item (a).
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema temos que obter o campo elétrico em um ponto a uma distância de um fio finito de comprimento e densidade de carga uniforme .
E ai, tem ideia de como fazemos isso? 🤔
Para obter o campo elétrico a partir de uma linha de carga, podemos aplicar a lei de Gauss dada por
Bora ver como essa equação se encaixa no nosso problema? 😁
Passo 2
Como o fio possui uma densidade de carga uniforme, o campo elétrico gerado por ele também ser�� uniforme, então podemos tirar da integral
Assim, podemos definir uma superfície gaussiana cilíndrica que envolve o fio e dizer que é a área superficial desse cilindro
Substituindo na equação de Gauss
Tranquilo até aqui? 👀
Passo 3
Nosso próximo passo é obter a carga envolvida .
Como temos uma densidade linear de carga, temos
Integrando nos dois lados, temos
Como é uniforme, podemos tirá-lo da integral
Substituindo na lei de Gauss
Porém, não é constante em todos os valores de , já que o fio é finito. Então temos
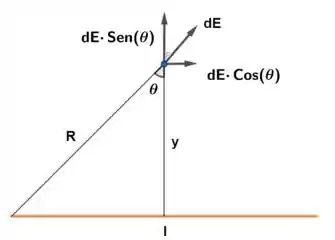
Perceba que para a variação de em todo do fio, as somas infinitesimais de se anulam, assim restando apenas a componente .
Portanto, temos que corrigir nosso resultado multiplicando pelo
Entendeu essa parte? 😉
Passo 4
E para o item b) temos que fazer a mesma análise para um fio infinito.
Pra isso podemos reaproveitar o resultado do item a) e fazer algumas análises.
Caso o fio fosse infinito, o problema seria exatamente até o ponto anterior que acrescentamos o ao campo.
Isso porque para o campo de um fio infinito, não seria necessário fazer aquela análise dos vetores de já que o ângulo do ponto ao fio não faria diferença.
Assim, o campo para um fio infinito é dado por
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
