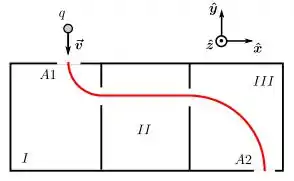
Uma partícula de carga se desloca inicialmente com velocidade constante . Num dado instante, ela entra através da abertura em uma caixa que é dividida em três regiões chamadas I, II e III, como mostra a figura abaixo. Nas regiões I e III a partícula é submetida somente a um campo magnético constante de mesmo módulo, enquanto na região II ela é submetida somente a um campo elétrico constante. Observa-se então que a partícula tem a trajetória indicada e sai da caixa através da abertura A2. Considerando que todo o movimento dela se dá no plano XY, qual é o sentido dos campos nas regiões I, II e III, respectivamente?
Passo 1
Bem, para esse problema temos apenas que ter em mente duas coisas...
- Regra da mão direita para o magnetismo.
- E que o campo elétrico atua sempre na direção de velocidade da carga positiva.
Então vamos nessa?
Passo 2
Quando a partícula entra...
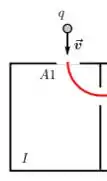
Ela tem a velocidade para baixo e uma força centrípeta que atua nela para cima...
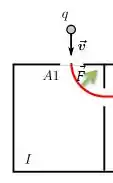
Então pela regra da mão direita para carga positiva, o campo magnético que gera essa força só pode estar para baixo...
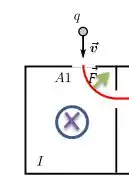
Ou seja, na direção negativa de ...
Passo 3
Já na região , a partícula de carga positiva vai se movimentar para a direita apenas se o campo elétrico tiver a mesma direção, isto é...
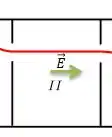
Na direção de positivo...
Passo 4
Por último, quando a partícula entra na terceira região, aparece uma força magnética que atua dessa vez para baixo...
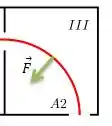
Logo, o campo magnético nessa região só pode ter sentido oposto ao campo magnético discutido no passo 2...
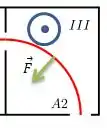
Ou seja, para cima, na mesma direção de positivo...
Resposta
Letra A.