Uma partícula carregada com carga se desloca com velocidade constante . Ela então entra através da abertura numa caixa que é dividida em duas partes (chamadas 1 e 2), onde podem ser aplicados campos magnéticos uniformes e estacionários em cada uma delas.
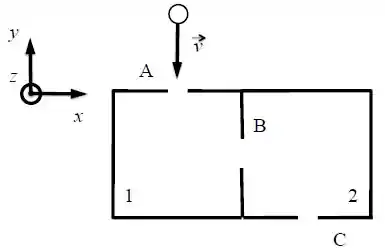
Na placa que separa as duas metades existe uma abertura para permitir a passagem da partícula. Observa-se que em seguida a partícula sai da caixa através da abertura C com a mesma velocidade .
Sejam e os módulos do campo magnético nas partes 1 e 2, respectivamente, com e . Dentre as opções abaixo, qual delas melhor descreve os vetores campo magnético nas duas partes da caixa?
e ;
e ;
e ;
e ;
e ;
Passo 1
Vamos dividir esse problema em duas partes, a primeira no movimento da partícula entre os pontos A e B, e a segunda no movimento da partícula entre os pontos B e C.
Quando a partícula entra em uma região com campo magnético uniforme e estacionário, a mesma percorrerá uma trajetória circular, onde a força magnética faz o trabalho de força centrípeta (apontando para o centro da trajetória circular).
Assim, a trajetória entre os pontos A e B deve ser a seguinte:
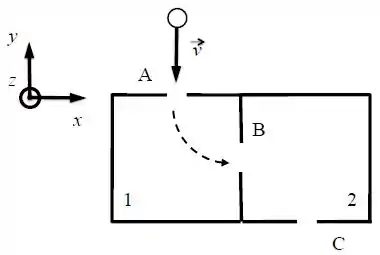
Lembrando que a força magnética deve apontar para o centro da trajetória circular e que o vetor velocidade é sempre tangente à trajetória, se pegarmos um ponto aleatório desse primeiro percurso, teremos:
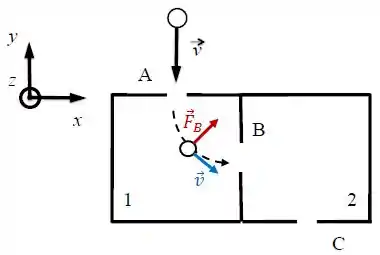
A força magnética sobre uma partícula carregada é dada por:
Como mostra o produto vetorial, o vetor campo magnético deve ser perpendicular aos vetores força magnética e velocidade em qualquer ponto da trajetória. Logo, ele deve estar entrando ou saindo do plano da página.
Para determinar isso, podemos utilizar a regra da mão direita, onde o dedo indicador deve estar na mesma direção e sentido do vetor velocidade (primeiro termo do produto vetorial), e o dedo polegar deve estar na mesma direção e sentido da força magnética (vetor resultante). Com isso, o dedo médio irá representar a direção e sentido do vetor campo magnético (segundo termo do produto vetorial).
Fazendo isso, chegamos à conclusão que o campo magnético deve estar no sentido .
Passo 2
Vamos fazer a mesma coisa para o trajeto entre os pontos B e C.
Agora, a trajetória circular entre os dois pontos deve ser a seguinte:
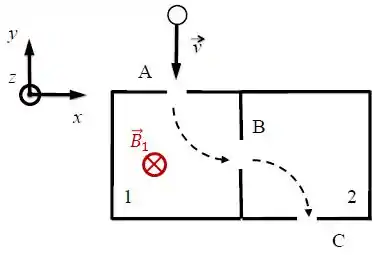
Novamente, posicionando os vetores força magnética (apontando para o centro da trajetória circular) e velocidade (sempre tangencial à trajetória), teremos:
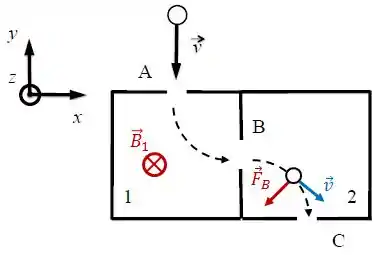
Utilizando novamente a regra da mão direita, concluímos que o campo magnético deve estar no sentido .
A resposta certa é a letra .
Resposta
e ;