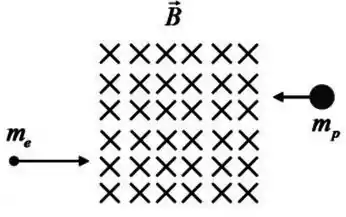
Um próton de massa , carga e velocidade com módulo igual a , junto a um elétron de massa , carga e velocidade com módulo entram numa região de campo magnético constante (uniforme e estacionário) de módulo , como mostrado na figura abaixo. Determine a razão entre o raio da orbita do próton () e o raio da órbita do elétron ()
(a)
(b)
(c)
(d)
(e)
Passo 1
Temos que o campo magnético é perpendicular às velocidades do elétron e do próton, assim os dois farão trajetórias circulares com a força magnética exercendo papel de força centrípeta. Assim
Assim para o próton
E para o elétron
Logo a razão pedida será
Resposta
(a)