USP, Sem Campus, Física 3, Listas de Física 3 - USP - Lista 1 - Lei de Coulomb, Campo Elétrico, Lei de Gauss, Questão 5
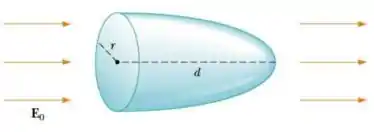
5) Em uma região do espaço existe um campo elétrico uniforme de magnitude . Calcule o fluxo do campo elétrico através da superfície paraboloide indicada na figura, notando que o eixo de simetria do paraboloide é paralelo ao campo elétrico.
Passo 1
Suave na nave?! Tá complicada essa questão? Relaxa que a gente vai te ajudar!
Nesse problema temos que obter o fluxo de um campo elétrico que passa em um paraboloide descrito na figura do problema.
Bem simples, né? 🤔
O campo elétrico tem modulo e o eixo de simetria do paraboloide é paralelo ao campo.
De forma geral, o fluxo elétrico é dado por
Lembra disso? 😉
Passo 2
Como e constante, podemos tirá-lo da integral
Mas o que é ? É a área da seção transversal do paraboloide, não é?
Mas por que a área da seção transversal? 🤔
Se olharmos pelo eixo simétrico do paraboloide, o que iriamos observar?
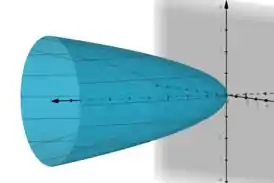
Como podemos ver, para o campo elétrico, a área transversal que ele está fluindo é um círculo. Então é muito mais fácil trabalharmos com a área do círculo do que com a área do paraboloide pois a rigor, para trabalharmos com o paraboloide, teríamos que parametrizar a sua superfície e obter o vetor normal a ela...
Então, como a base do paraboloide tem raio , a área da seção perpendicular ao campo será uma circunferência de raio .
Como a área da circunferência é dada por
Então
E finalmente, o fluxo é dado por
O que achou? Foi de boa? Responde aí! 😊
