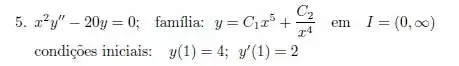
Passo 1
Para verificar se
É solução da equação, precisamos encontrar suas derivadas.
E
Substituindo as derivadas na EDO ficamos com
Logo, essa é de fato uma solução da equação.
Passo 2
Para encontrar as constantes e , basta aplicarmos as condições iniciais na solução e na derivada.
E
Resolvendo o sisteminha encontramos
E a solução única do PVI será
Resposta
Exercícios de Livros Relacionados
Os psicólogos interessados em teoria do aprendizado estudam as curvas do aprendizado. Uma curva de aprendizado é o gráfico de uma função P ( t ) , o desempenho de alguém aprendendo uma habilidade como
Use um sistema de computação algébrica para desenhar um campo de direções para a equação diferencial dada. Obtenha uma impressão e esboce uma curva solução que passe por (0, 1). Use o SCA para desenha
Use um sistema de computação algébrica para desenhar um campo de direções para a equação diferencial dada. Obtenha uma impressão e esboce uma curva solução que passe por (0, 1). Use o SCA para desenha
Use o campo de direções I para esboçoar os gráficos das soluções que satisfazem as condições iniciais dadas.a) y 0 = 1 b) y 0 = 0 c) y 0 = - 1
Nos Exercícios 5 e 6, copie os campos de direção e esboce algumas das curvas integrais. y ' = y y + 1 y - 1