UFMG, Sem Campus, Equações Diferenciais B, Listas de EDB - Prof° Aniura Milanés - Exercícios de EDB - 2021.1, Questão 16a
Calcule a série de Fourier das funções a seguir, definidas no intervalo .
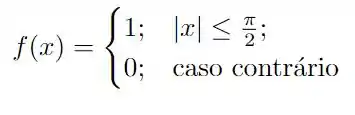
Passo 1
Eaew, tudo certinho?
Precisamos calcular a série de Fourier da seguinte função
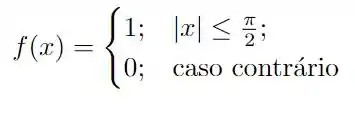
para isso, iremos calcular os coeficientes de Fourier
e, substituí-los na expressão
Bora lá!
Passo 2
Temos a seguinte função
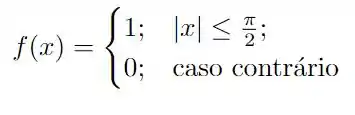
essa função é simplesmente no intervalo , e para e para . Portanto, essa é uma função de paridade par, de forma que o coeficiente do seno é nulo! E, precisamos calcular os outros coeficientes como
Essa integral pode ser identificada diretamente como
Vamos calcular agora os coeficientes dos cossenos!
Passo 3
Vamos calcular agora
A integral é tal que
ou seja, temos que para , inteiros pares, os coeficientes são zero, e temos que
Vamos finalmente escrever a nossa série!
Passo 4
Temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!