a) Esboce o gráfico da função dada por 3 períodos
b) Encontre a série de Fourier da função dada
Passo 1
a)
Para fazer o gráfico de , primeiro nós desenhamos os dados que estão nos colchetes (que valem em ), como fizemos em vermelho.
Depois, é só repetir esse desenho para a esquerda e para a direita (a cada a função se repete).
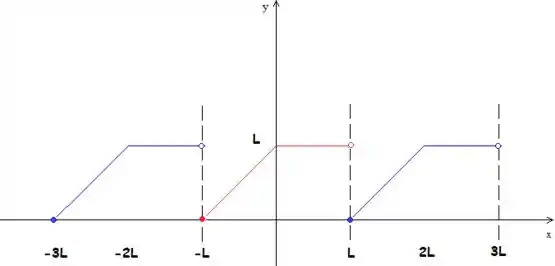
Passo 2
Letra b)
Precisamos agora encontrar a Série de Fourier de , temos o seguinte:
Como , sabemos que o período da função é , esse é o intervalo em que ela se repete. Lembra que a função representada por Série de Fourier tem que ser periódica? Então o da nossa fórmula é o mesmo da função.
Passo 3
Agora vamos calcular
Fazendo na expressão de temos:
Veja no gráfico, que de a temos duas expressões diferentes para , então o único jeito é dividir essa integral em duas, olha só:
Repare nos intervalos que escrevemos! A função vale em e em . Resolvendo essas integrais, temos
Passo 4
Agora vamos calcular os outros ’s. Temos que:
Dividindo essa integral em duas, como fizemos com :
Agora vamos integrar por partes, ok? Fazendo
Como o cosseno é uma função par:
Agora vamos analisar com calma. Perceba que
Logo
Guarde isso!
Obs: sempre que você encontrar um cosseno na expressão do ou do , faça essa análise!
Passo 5
Agora só falta calcular os ’s
Dividindo essa integral em duas:
Agora vamos fazer a integração por partes:
Lembrando que
Temos
Passo 6
Agora vamos substituir tudo o que encontramos, temos:
Vamos separar a série em duas para ver melhor:
Agora vamos com calma. Não podemos escrever direto no somatório porque isso só vale para ímpar. Vamos definir no primeiro somatório, então, , porque isso garante que temos índices ímpares, ok? Para temos , portanto a série deve começar em .Temos então
Agora vamos substituir o valor de usando a notação também, só para ficar igual à primeira série
Já que as duas séries possuem os mesmos índices, podemos juntá-las, não é?