UNB, Sem Campus, Cálculo 2, Listas de Fundamentos Matemáticos da Física B - Listas de Exercícios 5, Questão 4
Mostre que
Passo 1
Oiie, tudo certinho contigo?
Temos que demonstrar que
bem… não tem muito mais o que dizer, precisamos resolver a integral imprópria acima! Existem diversas maneiras de resolver esse problema, uma que eu estou um pouco mais confortável em apresentar para vocês é utilizar expressões em série de potências conhecidas que podem nos ajudar a simplificar o problema! Bora lá!
Passo 2
A função seno pode ser aproximada para a seguinte expressão em série de potências
usando isso em nosso integrando, temos que
Mas qual a vantagem disso? Como temos que a soma está em , e não em , podemos tirar a somatória da integral junto com alguns termos para obter
Agora, usando propriedades da exponenciação, podemos escrever que , de forma, que nossa integral se torna um pouco mais simples
Vamos tentar resolver isso agora! Vem comigo!
Passo 3
A integral restante também é tabelada e pode ser encontrada em uma lista de integrais exponenciais (junto com integrais gaussianas por exemplo), essa em particular obedece a seguinte relação
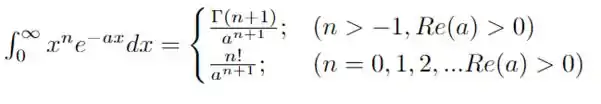
Note que temos que , um inteiro e , portanto, a nossa expressão se torna
De forma que nossa integral original é simplesmente
em que usei na última igualdade que . A série que restou também é conhecida, ela é a fórmula de Leibniz para , que pode ser identificada diretamente como
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!