UFMG, Sem Campus, Equações Diferenciais B, Listas de EDB - Prof° Aniura Milanés - Exercícios de EDB - 2021.1, Questão 73d
Determine a transformada de Fourier das funções a seguir utilizando a tabela de transformadas vista em sala de aula.
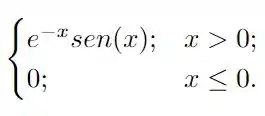
Passo 1
Oiie, tudo bem com você?
Nesta questão temos que calcular a transformada de Fourier de uma função da forma
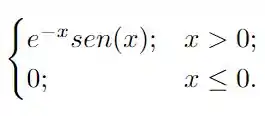
para isso devemos usar uma tabela de transformadas conhecidas! O enunciado indica uma tabela oficial nas notas de aula, mesmo sem ter acesso a esta tabela, existem resultados conhecidos que irei utilizar, belezinha? Nesta questão devemos partir do resultado
e, também usar a propriedade
Vamos tentar usar esses resultados! Saca só!
Passo 2
Se identificarmos que na equação , temos que , então temos que na equação , e a transformada é tal que
Mas, nossa função é multiplicada por um seno, sendo assim, precisamos aplicar a propriedade , como temos em nossa função simplesmente , temos que , a nossa transformada final é dada então por
que pode ser simplificada como
Ou simplesmente
A questão foi isso! Te vejo na próxima! Tchau Tchau!