UFMG, Sem Campus, Equações Diferenciais B, Listas de EDB - Prof° Aniura Milanés - Exercícios de EDB - 2021.1, Questão 71a
Seja
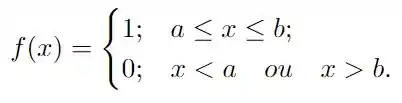
Calcule a transformada de Fourier .
Passo 1
Eaew, belezinha?
Precisamos calcular a transformada de Fourier da seguinte função
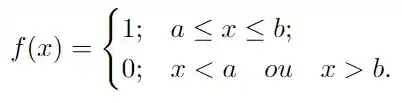
a definição para que façamos este cálculo é tal que
vamos aplicar a definição e resolver a integração! Vem comigo!
Passo 2
Aplicando a nossa função na definição da transformada, temos simplesmente
esta é uma integral de exponencial, portanto, temos que
A primeira alternativa foi essa! Te vejo na próxima! Tchau Tchau!
Resposta
Exercícios de Livros Relacionados
Uma série de Fourier finita é dada pela soma f x = ∑ n = 1 N a n s i n ( n x ) = a 1 sin x + a 2 sin 2 x + … + a N sin N x Mostre que o m - ésimo coeficiente a m é dado pela fórmula a m = 1 π