UFMG, Sem Campus, Equações Diferenciais B, Listas de EDB - Profª Aniura Milanés - Exercícios de EDB - 2021.1, Questão 27c
Obtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Passo 1
Faaaala galerinha do bem, tudo na paz com vocês?
Nessa questão recebemos a função:
E, precisamos calcular a série de Fourier de apenas em cossenos.
Sempre que queremos obter uma série de Fourier apenas em cossenos, precisamos que a função esteja definida como uma função par e periódica.
A função dada, quando definida nos reais, já é uma função par. Então, precisamos apenas defini-la de modo que ela também seja periódica. Beleza?
Depois disso, podemos seguir a ideia normal de série de Fourier de funções pares. Temos que:
onde:
Tranquilo até aqui? Vem comigo que vai ficar ainda mais claro!!
Passo 2
Bom, pra começar, vamos definir de modo que ela seja periódica. A definição dada no enunciado, é válida para:
Mas, no contexto das séries de Fourier, o período da função é dado por . Então, vamos ampliar a definição de , de modo que ela permaneça sendo par e também se torne periódica.
com periódica de período .
Uma observação rápida galera:
Quando definimos a função dessa forma, significa que estamos desenhando a curva no intervalo e para os outros pontos dos reais, apenas vamos “colando” a mesma curva. Isso basicamente é um modo de definir a facilitar o formalismo matemático.
Caso contrário, precisaríamos escrever algo do tipo:
E, assim por diante pra infinitos trechos... Agora sacaram porque apenas escrevemos a definição no intervalo e dizemos que ela é periódica de período ?
Perfeito! Vamos então desenhar o seu gráfico no intervalo :
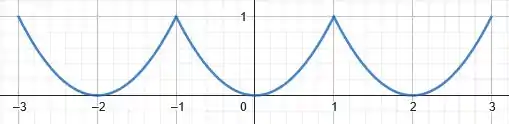
Passo 3
Agora precisamos calcular efetivamente a nossa série de Fourier em senos de . Para isso precisamos calcular os coeficientes :
Para resolver a integral acima precisamos utilizar o método de integração por partes. Bora dar uma rápida revisada nele:
Daí, fazendo:
Temos:
Como , temos:
Logo:
Precisamos resolver a integral:
Assim, fazendo:
Logo, temos:
Daí, vamos analisar. Como , temos que:
Ficamos só com o primeiro termo:
Daí, quando tivermos:
Podemos escrever:
Logo:
Daí, substituindo na expressão de :
OPA OPA OPA! Pera lá... se temos um problema nessa expressão!!
Passo 4
Vamos então voltar para a integral que define e colocar desde lá para calcularmos
Podemos então, finalmente escrever a nossa série de Fourier:
É isso pessoal! Muito obrigado pela atenção 😉