Determine a série de Fourier da função definida por
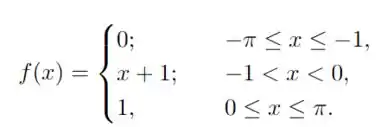
Passo 1
Oiie, tudo bem com você?
Precisamos calcular a série de Fourier da função
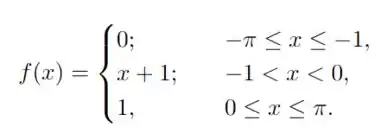
ela é uma função seccionalmente contínua e periódica, portanto, a série de Fourier com o seguinte formato
converge para a nossa função. Em nosso caso temos que , e os coeficientes são dados por
Bora rodar a manivela! Calcular essas integrais! Vem comigo!
Passo 2
Primeiro para o coeficiente , temos que
podemos usar a regrinha
para resolver as integrais como
O esquema para os outros coeficientes é o mesmo. Só as integrais que mudam um pouquinho. Bora lá!
Passo 3
Calculando agoras os coeficientes de cosseno, temos que
ou simplesmente
As integrais de cosseno poe ser identificadas como
portanto, temos os dois resultados
e, para a outra, temos que
A integral que sobra é um produto de um polinômio com uma função trigonométrica, então temos que resolvê-la por partes! Saca só!
Passo 4
A integração por partes é resolvida tomando que
em que podemos escolher quem será e , tomando a ordem de prioridade LIPTE (Logaritmo, Inversas, Polinomiais, trigonométricas e Exponencial), em que a ordem que aparece anteriormente nos diz quem é a prioridade para escolhermos como , portanto, em nosso caso temos que
e
de forma que
e
Ou seja, a nossa integral se torna
a segunda integral é identificada como
usando a paridade do cosseno, podemos dizer que
e, portanto, temos que
Finalmente, nosso coeficiente é tal que
Vamos calcular o coeficiente que falta agora! Vem comigo!
Passo 5
O último coeficiente é tal que
analogamente ao que fizemos no passo anterior, temos duas integrais que podemos identificar diretamente, sendo elas
e, a outra
A integral por partes também é feita de maneira parecida, escolhendo que
e
temos que
e
Portanto, a integral se torna
Usando que
em que usei a paridade da função seno! Podemos escrever que
simplificando algumas coisinhas, temos que
Agora só precisamos escrever a nossa série! Bora lá!
Passo 6
Aplicando todos os coeficientes em nossa série de Fourier temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!