UFV, Sem Campus, Cálculo 2,Trabalhos para Nota - 2022.2, Questão 4
Esboce o gráfico da função definida por
em que a série do segundo membro é a série de Fourier da função , periódica de período , dada por
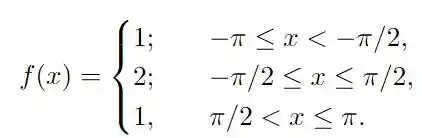
Justifique a construção do seu gráfico.
Passo 1
Oiie, tudo bem com você?
Precisamos esboçar o gráfico da função
sabendo que a série é em questão é a série de fourier da função
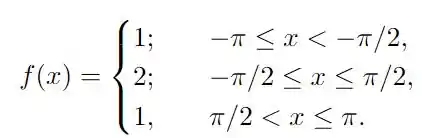
Essa questão é bastante direta se lembrarmos o teorema de convergência das séries de Fourier, bora relembrar? Vem comigo!
Passo 2
O teorema de convergência das séries de Fourier garante que se temos uma função periódica, e seccionalmente contínua, podemos garantir que a série de Fourier dada por
converge para , portanto, como temos que a função dada é seccionalmente contínua e periódica de período , podemos esboçar o gráfico como
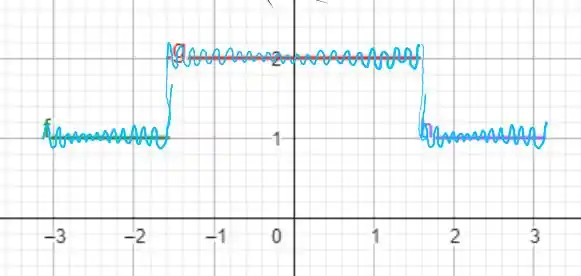
As oscilações surgem devido ao caráter trigonometria das séries de Fourier, note que quanto mais termos colocar, mais próximo de sua função estará! A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos Passos!