UFMG, Sem Campus, Equações Diferenciais B, Listas de EDB - Prof° Aniura Milanés - Exercícios de EDB - 2021.1, Questão 16c
Calcule a série de Fourier das funções a seguir, definidas no intervalo .
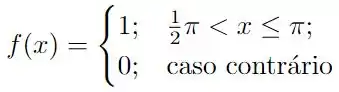
Passo 1
Eaew, tudo certinho?
Precisamos calcular a série de Fourier da seguinte função
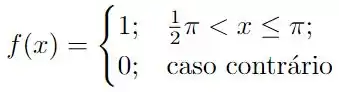
para isso, iremos calcular os coeficientes de Fourier
e, substituí-los na expressão
Bora lá!
Passo 2
Temos a seguinte função
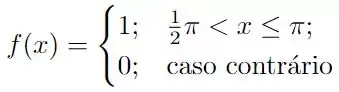
essa função é simplesmente no intervalo , e para . Portanto, essa é uma função sem paridade definida, de forma que temos que calcular todos os coeficientes, temos que
Essa integral pode ser identificada diretamente como
Vamos calcular agora os coeficientes dos cossenos!
Passo 3
Vamos calcular agora
A integral é tal que
portanto, temos que
Vamos calcular agora os coeficientes de seno!
Passo 4
Temos que calcular
o resultado é então da forma
A série é então dada por
A questão é isso! Te vejo na próxima! Tchau Tchau!