UFMG, Sem Campus, Equações Diferenciais B, Listas de EDB - Prof° Aniura Milanés - Exercícios de EDB - 2021.1, Questão 71b
Seja
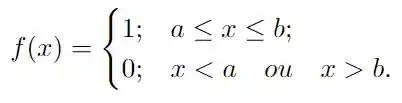
Qual relação deve haver entre e para que a parte imaginária de valha zero para qualquer calor de ?
Passo 1
Eaew, belezinha?
Temos definida a seguinte função
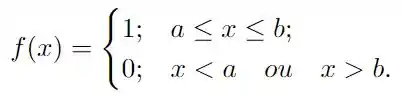
na alternativa anterior calculamos a sua transformada de Fourier como
Vamos usar esse formato calculado para encontrar uma relação entre e de forma que
Bora lá!
Passo 2
Queremos que
como temos que é qualquer, precisamos achar uma condição tal que
ou simplesmente
aplicando o logaritmo neperiano em ambos os lados, temos que
Portanto, precisamos que
Aí está! A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Exercícios de Livros Relacionados
Uma série de Fourier finita é dada pela soma f x = ∑ n = 1 N a n s i n ( n x ) = a 1 sin x + a 2 sin 2 x + … + a N sin N x Mostre que o m - ésimo coeficiente a m é dado pela fórmula a m = 1 π