UFMG, Sem Campus, Equações Diferenciais B, Listas de EDB - Profª Aniura Milanés - Exercícios de EDB - 2021.1, Questão 26c
Obtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Passo 1
Faaaala galerinha do bem, tudo na paz com vocês?
Nessa questão recebemos a função:
E, precisamos calcular a série de Fourier de apenas em senos.
Sempre que queremos obter uma série de Fourier apenas em senos, precisamos que a função esteja definida como uma função ímpar e periódica.
O problema é que, a função , quando definida nos reais, não é nem ímpar nem periódica...
Nessas situações precisamos expandir o intervalo de definição de (observa que nesse problema ela foi definida apenas em ) de modo a torná-la ímpar e periódica.
Depois que fizermos isso, podemos usar a teoria normal da série de Fourier pra funções ímpares e periódicas pra encontrar a sua expansão:
onde:
Tranquilo até aqui? Vem comigo que vai ficar ainda mais claro!!
Passo 2
Bom, primeiramente precisamos pensar numa definição de que a torne ímpar e periódica.
Podemos escrever:
onde é periódica de período .
Isso significa que pra desenhar a curva de à esquerda e à direita de e , respectivamente, basta “colar” a mesa curva que aparece no intervalo . Assim, conseguimos de um jeito simples expandir a definição da nossa função pra todos os reais, e ainda forçando ela a ser ímpar e periódica. Sacaram?
Vamos então desenhar o seu gráfico no intervalo :
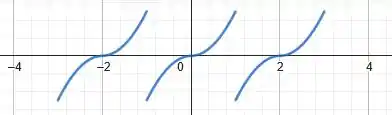
(pra fins de gráfico consideramos , sem perda de generalidade, beleza?).
Perfeito! A gente pode até dá uma conferida que nossa função realmente é ímpar e periódica, não é mesmo 😊
Passo 3
Vamos agora calcular os coeficientes da nossa série de Fourier. Temos que:
Para resolver essa integral precisamos usar o método de integração por partes. Vamo dar uma revisada:
No caso da nossa integral, vamos chamar:
Assim:
O problema é que essa segunda integral também precisa ser calculada usando o método de integração por partes, daí fazendo:
Temos:
Como , temos que:
Assim:
Beleza, substituindo isso na nossa equação principal do cálculo da integral, temos:
Como:
Então,
- Se par:
- Se ímpar:
Perfeito!
Logo, para o coeficiente , vamos ter:
- par:
- ímpar:
Logo, podemos escrever a série de Fourier de como sendo:
(separamos em dois somatórios: um para par (e chamamos de ), e outro para ímpar (e chamamos de ).
Pronto, é só esse monstrinho daí 😉
Espero que vocês tenham entendido bem direitinho, até a próxima 😊