UFMG, Sem Campus, Equações Diferenciais B, Listas de EDB - Profª Aniura Milanés - Exercícios de EDB - 2021.1, Questão 27e
Obtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Passo 1
E aí gente, tudo bem com vocês?
Nessa questão recebemos a função:
E, precisamos determinar a sua série de Fourier apenas em cossenos.
Sempre que queremos obter uma série de Fourier apenas em cossenos, precisamos que a função esteja definida como uma função par e periódica.
O problema é que a função dada não é nem par nem periódica no intervalo em que foi definida. Lembra que pra uma função ser par ela precisa obedecer:
E, isso não é obedecido para .
Nessas situações precisamos expandir o intervalo de definição de (observa que nesse problema ela foi definida apenas em ) de modo a torná-la par e periódica.
Depois disso, podemos seguir a ideia normal de série de Fourier de funções pares. Temos que:
onde:
Tranquilo até aqui? Vem comigo que vai ficar ainda mais claro!
Passo 2
Bom, pra começar vamos definir de modo que ela seja par e periódica.
Pra ela ser par, precisa ser obedecido:
Então, . Assim, para definir nossa função no intervalo , basta trocarmos por na expressão acima:
Daí, podemos definir como:
com periódica de período .
Uma observação rápida galera:
Quando definimos a função dessa forma, significa que estamos desenhando a curva no intervalo e para os outros pontos dos reais, apenas vamos “colando” a mesma curva. Isso basicamente é um modo de definir a facilitar o formalismo matemático.
Caso contrário, precisaríamos escrever algo do tipo:
E, assim por diante pra infinitos trechos... Agora sacaram porque apenas escrevemos a definição no intervalo e dizemos que ela é periódica de período ?
Perfeito! Vamos então desenhar o seu gráfico no intervalo :
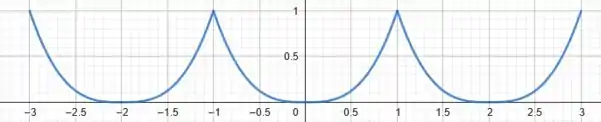
(consideramos para fins do gráfico, sem perda de generalidade).
onde se anula para todo .
Perfeito! Temos par e periódica.
Passo 3
Agora vamos calcular efetivamente a série de Fourier de . Para isso precisamos calcular os coeficientes :
Galera, em geral, aparece um problema quando colocamos , pois durante a integração acaba aparecendo um no denominador. Então, vamos começar calculando separadamente, e depois calculamos para um qualquer ().
Agora sim, vamos para o cálculo de com . Precisamos resolver a integral:
Para isso, vamos utilizar o método de integração por partes. Dando uma rápida revisada nele, temos:
Assim, fazendo:
Temos:
Como dado que , vem que:
Para resolver essa integral também vamos utilizar o método de integração por partes.
Show de bola!
Passo 4
No caso da nossa integral, vamos chamar:
Assim:
O problema é que essa segunda integral também precisa ser calculada usando o método de integração por partes, daí fazendo:
Temos:
Como , temos que:
Assim:
Beleza, substituindo isso na nossa equação principal do cálculo da integral, temos:
Como:
Então,
- Se par:
- Se ímpar:
Substituindo esses resultados em , temos:
- Se é par:
- Se é ímpar:
Perfeito!
Assim, podemos finalmente escrever a série de Fourier de . Lembrando que:
Temos:
(Separamos o somatório nos termos pares, onde trocamos por e nos termos ímpares, onde trocamos por .)
Prontinho galera! Terminamossss!!
Curtiram a solução? Responde Aí!