UFMG, Sem Campus, Equações Diferenciais B, Listas de EDB - Profª Aniura Milanés - Exercícios de EDB - 2021.1, Questão 27a
Obtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Passo 1
Faaaala pessoal, tudo bem com vocês?
Nessa questão recebemos a função:
E, precisamos obter a série de Fourier em cossenos dessa função.
Puts!!! A função seno é uma função ímpar, mas pra obtermos uma série de Fourier apenas em cossenos precisamos estar tratando de uma função par e periódica. Será que o enunciado tá errado?
Nãooooo hahaha... é um tipo de probleminha mais complicado mesmo, mas tem uns truques bem legais que vamos aprender, então vem comigo!
A ideia principal pra conseguir escrever uma série de Fourier apenas de cossenos para uma função qualquer, é que podemos estender o gráfico da função dada, definindo ela por partes, de modo a forçá-la a ser par.
Depois disso, podemos seguir a ideia normal de série de Fourier de funções pares. Temos que:
onde:
Tranquilo até aqui? Vem comigo que vai ficar ainda mais claro!!
Passo 2
Bom, precisamos começar ajustando a definição.
Queremos definir a função seno em um intervalo mais amplo de modo que ela seja par. Vamos então, inicialmente, tratar dessa definição no intervalo .
Temos que:
Assim, temos:
Dessa forma temos a função sendo par. Daí, podemos escrever a sua definição:
onde diremos que é periódica e, a princípio, de período . (Dizemos a princípio, porque essas funções trigonométricas às vezes possuem algumas simetrias interessantes, que quando expandimos o intervalo desse modo, temos um período menor do que . Pra saber disso direitinho, vamos desenhar o gráfico).
Primeiramente, vamos desenhá-lo no intervalo . Temos:
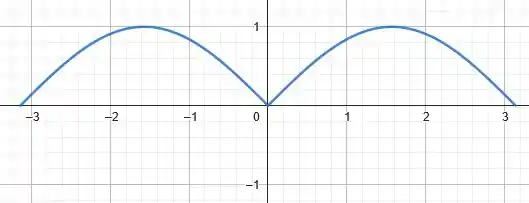
Olha aí, o que havíamos comentado. Embora tenhamos definido a função no intervalo , ao desenhar o gráfico vemos que o período de é .
E, no contexto da série de Fourier, temos que:
Ou seja, o período da função é . Logo, no caso da nossa , vem:
Assim, precisamos desenhar o gráfico dessa função no intervalo . Vamos ter:
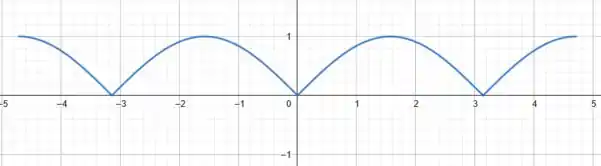
Prontinho pessoal! Vamos para a próxima parte do exercício 😊
Passo 3
Agora precisamos determinar efetivamente a série de Fourier em cossenos da função . Para fazer isso, precisamos determinar os coeficientes que multiplicam a nossa função cosseno. Temos:
Massa! Então, nossa missão é resolver essa integral.
Podemos usar a fórmula da transformação de produto em soma da trigonometria:
Daí, temos:
Logo:
Daí:
Reescrevendo a integral, temos:
Resolvendo as integrais:
Substituindo os limites de integração:
Substituindo de volta no coeficiente , temos:
Logo:
Se , temos:
Portanto, podemos escrever a série de Fourier de como:
E é isso galerinha! Curtiram a solução?
Responde Aí!