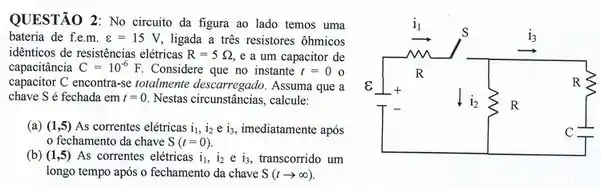
Passo 1
Letra (a).Imediatamente após o fechamento da chave, o capacitor conta como um fio, sem tensão nenhuma. Isso ocorre porque existe inércia na tensão do capacitor, mas não existe inércia em sua corrente. De forma que a corrente do capacitor pode sofrer variações bruscas.
Então, quando fechamos a chave, a fonte de tensão “vê” uma resistência em série com duas resistências em paralelo. A resistência equivalente disso é:
Dessa forma, a corrente vai valer:
Essa corrente se divide entre dois resistores de resistência iguais e, por isso:
Passo 2
Letra (b). Após um longo período de tempo, o capacitor se carrega completamente e não passará mais corrente sobre ele. Por isso, para temos:
Dessa forma, apenas a malha da esquerda está ativa e, por isso:
Resposta
Letra (a)
Letra (b)