Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuito RC

Ver Teoria
Exercício 67123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566686970717273747576777879808182

Enunciado

Circuitos

No circuito da figura, o capacitor está inicialmente descarregado.

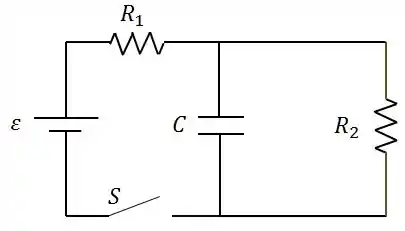
  1. Imediatamente após a chave S ser fechada, qual é a corrente no resistor R 1 ?
  2. Qual é a potência dissipada no resistor R 1 ?
  3. Transcorrido um tempo muito longo após o fechamento da chave S , qual é a energia acumulada no capacitor?
  4. Abrindo-se a chave S , qual é a corrente no resistor R 2 em função do tempo?
  5. Qual é a energia total dissipada no processo de descarga do capacitor?

Passo 1

  1. Imediatamente após a chave S ser fechada, qual é a corrente no resistor R 1 ?

    2. Assim que a chave é fechada, não existe diferença de potencial entre os terminais do capacitor, já que ele está descarregado... isso significa que quando a corrente “chega” no nó, logo após passar por R 1 , ela vai toda para o ramo do capacitor.

    Logo:

    ε = R 1 i 0

    i 0 = ε R 1

    Passo 2

  2. Qual é a potência dissipada no resistor R 1 ?

    3. A potência dissipara em R 1 será:

    P = ε 2 R 1

    Só isso? Sim... só isso.

    Passo 3

  3. Transcorrido um tempo muito longo após o fechamento da chave S , qual é a energia acumulada no capacitor?

    4. A energia acumulada em um capacitor é dada por:

    U = Q 2 2 C

    Onde C é a capacitância desse capacitor.

    Depois de um tempo muito longo, o capacitor estará totalmente carregado e a corrente parará de passar por ele. Nesse ponto, a carga do capacitor (máxima) é dada por:

    Q m = C V C

    Como o capacitor e R 2 estão em paralelo, a diferença de potencial V C pode ser escrita como:

    V C = R 2 i 1

    Beleza, então precisamos encontrar uma nova expressão para a corrente... isso vai desencadear todo o resto até chegarmos na resposta, ok?

    Passo 4

    Quando o capacitor esta totalmente carregado a corrente i 1 passará completamente por R 2 , logo:

    ε - R 1 + R 2 i 1 = 0

    i = ε R 1 + R 2

    Agora sim!

    V C = R 2 i = R 2 ε R 1 + R 2

    Q m = C V C = R 2 C ε R 1 + R 2

    Por fim, a energia é dada por:

    U = Q 2 2 C

    U = R 2 2 C 2 ε 2 2 C R 1 + R 2 2

    U a r m a z e n a d a = C ε 2 R 2 2 2 R 1 + R 2 2

    Passo 5

  4. Abrindo-se a chave S , qual é a corrente no resistor R 2 em função do tempo?

    5. Quando abrirmos a chave novamente, o capacitor começará a descarregar. Nesse regime, a corrente i 2 que passa por ele será dada por:

    i 2 = - Q m R 2 C e - t R 2 C

    Onde:

    Q m = R 2 C ε R 1 + R 2

    Logo:

    i 2 = - 1 R 2 C   R 2 C ε R 1 + R 2 e - t R 2 C

    i 2 = - ε R 1 + R 2 e - t R 2 C

    O sinal negativo aqui é só pra lembrar que a corrente agora vai fluir no sentido contrário ao que vinha antes. Agora ela passará a fluir no senti anti-horário.

    Passo 6

  5. Qual é a energia total dissipada no processo de descarga do capacitor?

A energia total dissipada será exatamente igual à energia acumulada pelo capacitor quando estava totalmente carregado.

U d i s s i p a d a = U a r m a z e n a d a = C ε 2 R 2 2 2 R 1 + R 2 2

Resposta

a.

i 0 = ε R 1

b.

P = ε 2 R 1

c.

U a r m a z e n a d a = C ε 2 R 2 2 2 R 1 + R 2 2

d.

i 2 = - ε R 1 + R 2 e - t R 2 C

e.

U d i s s i p a d a = C ε 2 R 2 2 2 R 1 + R 2 2

Exercícios de Livros Relacionados

O capacitor C da Figura 25-49 está inicialmente descarregado. Logo após o interruptor S ser fechado, (a) a tensão em C é igual a E, (b) a tensão em R é E. (c) a corrente no circuito é zero, (d) ambas
O circuito mostrado na figura abaixo é uma ponte de Wheatstone e o resistor variável está sendo usado como um potenciômetro de fio deslizante. A resistência R 0 é conhecida. Esta “ponte” PE usada para
Mostre que a Equação d Q d t = ℇ C - Q R C ℇ pode ser reescrita como d Q ℇ C - Q = d t R C ℇ . Integre esta equação para derivar a solução dada pela Equação Q f ( 1 - e - t / R C ) .
No circuito mostrado na figura abaixo, o capacitor tem capacitância de 2.50 μ F e o resistor tem resistência de 0.500M Ω . Antes de a chave ser fechada, a queda de potencial no capacitor é 12.0V , com
A Fig. 27-67 mostra dois circuitos com um capacitar carregado que pode ser descarregado através de um resistor quando uma chave é fechada. Na Fig. 27-67a, R 1 = 20,0 Ω e C 1 = 5,00 μ F . Na Fig. 27-67