Considere o circuito mostrado na figura. Na figura, a força eletromotriz , as resistências e e a capacitância . No início a chave está aberta e o capacitor está descarregado. No instante fechamos a chave.
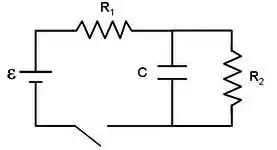
(a) Calcule a corrente passando nos resistores e no instante .
(b) Calcule a corrente passando nos resistores e após um tempo longo o suficiente para o sistema atingir o regime estacionário.
(c) Calcule a potência dissipada no resistor nesse regime estacionário.
Passo 1
No instante , sabemos que o capacitor se comporta como um curto circuito. Como está em paralelo com , a corrente que passa por será nula, certo?
Já a corrente que passa por é calculada como:
Passo 2
Quando o sistema atinge o regime estacionário, o capacitor irá se comportar como um circuito aberto. Isso significa que a corrente que passa por ele é nula, enquanto que a corrente que passa pelo resistor é a mesma que a corrente que passa pelo resistor .
Temos:
Passo 3
A potência dissipada no resistor é calculada como:
Resposta
(a) e .
(b) .
(c) .