O circuito abaixo apresenta capacitores de capacitância , inicialmente descarregados, e resistores de resistência . A força eletromotriz do circuito vale e a chave Ch está inicialmente aberta. Assinale a alternativa falsa.
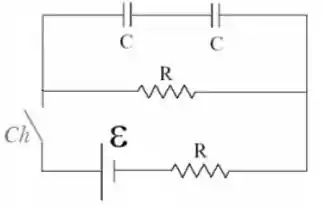
- No instante em que se fecha a chave, a intensidade da corrente que atravessa o resistor do ramo central é nula.
- Depois de muito tempo que a chave foi fechada, com os capacitores totalmente carregados, a ddp em cada resistor será igual a .
- Depois de muito tempo que a chave foi fechada, os capacitores estão totalmente carregados.
- Depois de muito tempo que a chave foi fechada, a intensidade da corrente nos resistores será igual a zero.
- Depois de muito tempo que a chave foi fechada, a corrente nos capacitores será igual a zero.
Passo 1
Aqui, é interessante dividirmos a análise do circuito em dois instantes de tempo: e . Bora fazer isso então...
TEMPO :
Vamos começar vendo que capacitância equivalente dos dois capacitores é :
Nesse instante de tempo, os dois capacitores ainda estão totalmente descarregados, o que significa que eles não têm carga, . Por essa razão, a ddp entre as extremidades do capacitor equivalente é zero, já que:
Como esse capacitor está em paralelo com o resistor logo abaixo, a diferença de potencial através de também será zero. Então, não passará corrente no resistor do meio.
Portanto, o item a) está correto.
Passo 2
TEMPO :
Nesse instante de tempo, ou seja, para um tempo muito grande, os capacitores estarão completamente carregados e por eles não passará mais nenhuma corrente elétrica.
Portanto, os itens c) e e) estão corretos.
Agora, a corrente para um tempo muito grande passará apenas pelos resistores em série e pela fonte de fem . Podemos encontrar essa corrente aplicando a lei das malhas para a malha que contém esses dois resistores em série:
que é diferente de zero.
Assim, o item d) está incorreto!
Para fechar, também para um tempo muito grande, a gente consegue também encontrar qual é a ddp entre de cada um dos resistores . A ddp neles será:
provando que o item b) está correto.
Resposta
Letra d.