(a)
(b) Zero
(c)
(d)
(e)
Após a chave ser ligada...
(a)
(b)
(c)
(d)
(e)
Passo 1
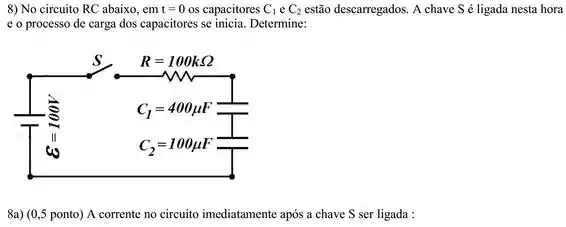
8a) Imediatamente após a chave ser fechada os capacitores se comportam como dois curtos-circuitos, como dois fios sem resistência. Então:
Passo 2
8b) Calcular a carga no capacitor equivalente. A primeira coisa é transformar os dois capacitores em um só e lembrar que:
- A capacitância em série a gente calcula que nem a resistência em paralelo
- A capacitância em paralelo a gente calcula que nem a resistência em série
Então, o lance é fazer o contrário da resistência! Vamos lá (na questão as capacitâncias estão em séries e temos que usar a fórmula da resistência em paralelo):
Passo 3
Calcular a carga no capacitor equivalente. Para fazer isso é usar na capacitância equivalente a definição mesmo de capacitância:
Sensacional, ficamos entre a letra (a) e a letra (e) ;)
Passo 4
A constante de tempo capacitiva é igual a :
Resposta
8a) (e)
8b) (e)
Exercícios de Livros Relacionados
O capacitor C da Figura 25-49 está inicialmente descarregado. Logo após o interruptor S ser fechado, (a) a tensão em C é igual a E, (b) a tensão em R é E. (c) a corrente no circuito é zero, (d) ambas
O circuito mostrado na figura abaixo é uma ponte de Wheatstone e o resistor variável está sendo usado como um potenciômetro de fio deslizante. A resistência R 0 é conhecida. Esta “ponte” PE usada para
Mostre que a Equação d Q d t = ℇ C - Q R C ℇ pode ser reescrita como d Q ℇ C - Q = d t R C ℇ . Integre esta equação para derivar a solução dada pela Equação Q f ( 1 - e - t / R C ) .
No circuito mostrado na figura abaixo, o capacitor tem capacitância de 2.50 μ F e o resistor tem resistência de 0.500M Ω . Antes de a chave ser fechada, a queda de potencial no capacitor é 12.0V , com
A Fig. 27-67 mostra dois circuitos com um capacitar carregado que pode ser descarregado através de um resistor quando uma chave é fechada. Na Fig. 27-67a, R 1 = 20,0 Ω e C 1 = 5,00 μ F . Na Fig. 27-67