Considere o circuito mostrado na figura.
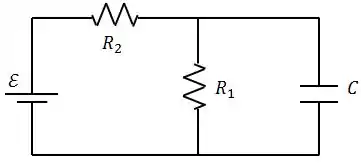
A fonte de fem tem resistência interna desprezível. Os resistores têm resistências e . O capacitor tem capacitância . Quando o capacitor está completamente carregado, o módulo da carga nas placas é .
O valor é:
;
;
;
;
;
Passo 1
Quando o capacitor está completamente carregado, a corrente elétrica para de circular pelo ramo onde o mesmo está.
Neste caso, a diferença de potencial através do capacitor é dada por:
Passo 2
Como o capacitor associado em está paralelo com o resistor , a diferença de potencial através do resistor também vale .
A partir disso, podemos calcular a corrente, dada por:
Passo 3
Finalmente, utilizando a Lei de Kirchhoff na malha que contém a fonte e os dois resistores, teremos:
Resposta
;
Exercícios de Livros Relacionados
O capacitor C da Figura 25-49 está inicialmente descarregado. Logo após o interruptor S ser fechado, (a) a tensão em C é igual a E, (b) a tensão em R é E. (c) a corrente no circuito é zero, (d) ambas
O circuito mostrado na figura abaixo é uma ponte de Wheatstone e o resistor variável está sendo usado como um potenciômetro de fio deslizante. A resistência R 0 é conhecida. Esta “ponte” PE usada para
Mostre que a Equação d Q d t = ℇ C - Q R C ℇ pode ser reescrita como d Q ℇ C - Q = d t R C ℇ . Integre esta equação para derivar a solução dada pela Equação Q f ( 1 - e - t / R C ) .
No circuito mostrado na figura abaixo, o capacitor tem capacitância de 2.50 μ F e o resistor tem resistência de 0.500M Ω . Antes de a chave ser fechada, a queda de potencial no capacitor é 12.0V , com
A Fig. 27-67 mostra dois circuitos com um capacitar carregado que pode ser descarregado através de um resistor quando uma chave é fechada. Na Fig. 27-67a, R 1 = 20,0 Ω e C 1 = 5,00 μ F . Na Fig. 27-67