Um capacitor de placas planas e paralelas de área , com separação , tendo o vácuo como meio dielétrico, é conectado a um gerador de força eletromotriz através da chave e de três resistores iguais , dispostos como na figura. O circuito possui também outros dois resistores , conectados ao capacitor através da chave .
Em todos os cálculos considere: (base dos logaritmos neperianos), .
Considere as seguintes fases:
Fase 1: a chave está aberta e a chave é fechada por um tempo e depois aberta novamente.
Fase 2: com a chave aberta, a chave é fechada por muito tempo.
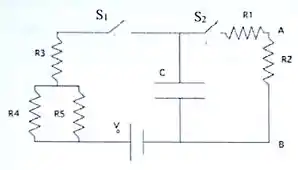
Determine:
(a) A capacitância do capacitor.
(b) A tensão e a carga do capacitor no final da Fase 1, ou seja, quando é aberta novamente. (Sugestão: analise a constante de tempo do circuito).
(c) A energia armazenada no capacitor durante o carregamento.
(d) A corrente que passa em e no instante de tempo após o início da Fase 2. (Sugestão: analise novamente a constante de tempo do circuito)
(e) A ddp (sobre ) no instante
(f) A energia total dissipada durante o descarregamento de até o instante
(g) A potência dissipada sobre e no instante
Passo 1
(a) A capacitância do capacitor.
A capacitância é dada por:
Passo 2
(b) A tensão e a carga do capacitor no final da Fase 1, ou seja, quando é aberta novamente. (Sugestão: analise a constante de tempo do circuito).
A tensão no capacitor em função do tempo pode ser escrita como:
Nesse caso, é a resistência equivalente ao combinar os resistores e em paralelo e esse resultado em série com . Assim sendo, .
Para , temos:
A carga no capacitor em função do tempo pode ser escrita como:
Passo 3
(c) A energia armazenada no capacitor durante o carregamento.
A energia armazenada no capacitor durante o carregamento é dada por:
Passo 4
(d) A corrente que passa em e no instante de tempo após o início da Fase 2.
A corrente que passa em e na Fase 2 é dada por:
onde é a resistência equivalente, dada por , e é a carga do capacitor no final da Fase 1 (começo da Fase 2), dada por .
No instante de tempo , temos:
onde o sinal de negativo na corrente significa que, agora, ela está fluindo no sentido oposto ao anterior, na Fase 1.
Passo 5
(e) A ddp (sobre ) no instante
A ddp sobre no instante é dada por:
Passo 6
(f) A energia total dissipada durante o descarregamento de até o instante
Vamos, inicialmente, calcular a carga no capacitor no instante :
A energia no capacitor neste instante é dada, então, por:
Assim sendo, a energia total dissipada durante o descarregamento de será dada por:
onde é a energia no final da Fase 1 (início da Fase 2), dada por .
Logo,
Passo 7
(g) A potência dissipada sobre e no instante
No instante , a corrente que passa pelos resistores e será:
como vimos no item (d).
Assim sendo, as potências e dissipadas por e são dadas por:
Resposta
(a)
(b) e
(c)
(d)
(e)
(f)
(g)