No circuito da figura, os capacitores têm as seguintes propriedades:
- : inicialmente descarregados, ambos com meio de constante dielétrica e capacitância de .
- : Carga inicial de , tipo placas paralelas com vácuo entre elas e de capacitância igual a .
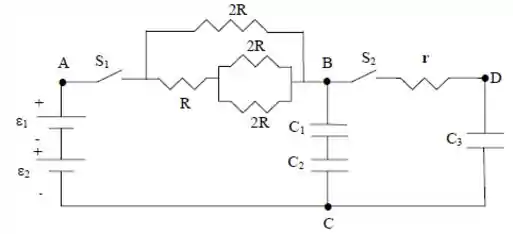
Nesse circuito, ocorrem as seguintes fases sucessivas:
- Fase 1: chave fechada e aberta durante longo tempo.
- Fase 2: Chaves abertas, o meio dielétrico de é substituído por vácuo e a separação das placas é alterada.
- Fase 3: chave aberta e fechada durante longo tempo.
Considerando , e , determine:
As d.d.p. em função do tempo durante a fase 1.
A carga em no final da fase 1.
Qual deve ser o aumento da separação das placas de durante a fase 2, para que a corrente no resistor seja nula durante toda a fase 3?
A diferença entre as energias armazenadas em na fase 1 e no final da fase 2.
Passo 1
As d.d.p. em função do tempo durante a fase 1.
Bom, na Fase 1, como a chave está aberta, o nosso circuito, basicamente, se resume a isso aqui:
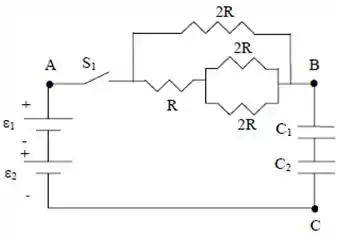
Antes de continuar aqui, vamos dar uma arrumada nessa bagunça.
Temos duas fontes aqui... a fonte equivalente será:
Pra resistência equivalente, começamos pelas duas resistências de em paralelo:
Essa resistência, em série com a outra resistência , resultará em uma resistência equivalente dessas duas:
Já resolvermos o ramo inferior desse cara. Finalmente, a resistência equivalente será:
Para a capacitância equivalente, como e estão em série:
Como .
Ótimo! Isso resultar em um circuito simples, mais ou menos com essa cara.
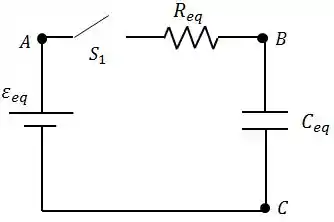
Passo 2
Ok, agora vamos dar uma olhada nas diferenças de potenciais.
- e
Esse trecho engloba o capacitor equivalente, que está inicialmente descarregado. A voltagem no capacitor enquanto ele está carregando é dada por:
Esse trecho engloba apenas o resistor, logo:
Passo 3
A carga em no final da fase 1.
Como os capacitores são iguais:
Passo 4
Qual deve ser o aumento da separação das placas de durante a fase 2, para que a corrente no resistor seja nula durante toda a fase 3?
No final da Fase 1, os capacitores e estavam totalmente carregados.
E o capacitor possui carga .
Na Fase 2, as chaves abertas, o meio dielétrico de é substituído por vácuo e a separação das placas é alterada.
, tanto se percorrermos o circuito passando pelos capacitores 1 e 2, quanto se percorrermos o circuito passando pelo capacitor 3, deve nos fornecer o mesmo valor.
Então é isso que vamos fazer, vamos percorrer esse caminho desses dois jeitos diferentes e igualá-los para descobrir quanto deve ser a separação das placas de .
Passo 5
Quando tirarmos o dielétrico de e , as suas capacitâncias irão mudar, de modo que:
Como :
Quando colocamos ou tiramos o dielétrico de um capacitor, as únicas coisas que mudam são a capacitância do mesmo e a ddp entre os seus terminais... a carga se mantém inalterada, logo:
Finalmente:
Agora vamos comparar com e descobrir a relação entre as separações .
Para um capacitor de placas planas e paralelas:
Como a única coisa que mudou foi a separação:
Logo, a nova separação entre as placas deve ser 5 vezes a separação inicial.
Passo 3
A diferença entre as energias armazenadas em na fase 1 e no final da fase 2.
A energia armazenada em um capacitor é dada por:
Lembra que no passo anterior nós já tínhamos achado a relação entre e ?
Voltando ao problema:
Onde e .
Resposta