O interruptor está na posição da figura por um longo tempo. No instante ele é trocado para a posição . Determine a carga do capacitor e a corrente no resistor nos tempos:
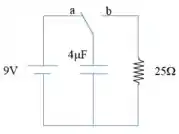
No instante em que a chave é fechada.
Passo 1
Para determinar a carga no capacitor quando a chave é fechada, precisamos lembrar da seguinte relação:
Onde é a diferença de potencial e é a capacitância, substituindo, temos:
A corrente no resistor é dada por:
Passo 2
Para determinar a carga no capacitor em diferentes tempos, precisamos lembrar da equação para a carga de um capacitor descarregando:
Onde é a carga inicial e e é a denominada constante de tempo capacitiva, como já temos a carga inicial, vamos então calcular :
Substituindo na equação, temos:
Já a corrente no descarregamento de um capacitor é dada por:
O sinal negativo da corrente na fórmula só indica que o seu sentido é contrário àquele do carregamento.
Passo 3
Para , temos:
Em módulo:
Passo 4
Para , temos:
Em módulo:
Resposta