Considere o circuito abaixo levando em consideração que a bateria é ideal, de força eletromotriz , e que o capacitor encontra-se descarregado inicialmente.
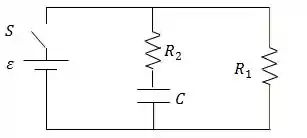
Após ligar a chave , no tempo , calcule:
- A corrente que passa pelo resistor ;
- A corrente que passa pela chave , imediatamente após ser ligada ;
- A carga do capacitor e a corrente que passa pelo resistor , em função do tempo;
Passo 1
a. A corrente que passa pelo resistor ;
Com o arranjo em paralelo, a diferença de potencial pelo ramo que passa por é . Logo:
Passo 2
b. A corrente que passa pela chave , imediatamente após ser ligada ;
Quando , o capacitor está totalmente descarregado, não causando diferença de potencial.
Nesse instante o circuito se comporta levando em consideração somente as resistências em paralelo, cuja resistência equivalente é dada por:
Assim, a corrente que passa pela chave será:
Passo 3
c. A carga do capacitor e a corrente que passa pelo resistor , em função do tempo;
Assim que a chave é fechada, o capacitor começa o processo de carregamento. Nesse momento, a sua carga varia com o tempo a partir de função:
Para determinarmos a corrente que passa pelo capacitor, temos apenas que derivar a função acima:
Resposta
a.
b.
c.