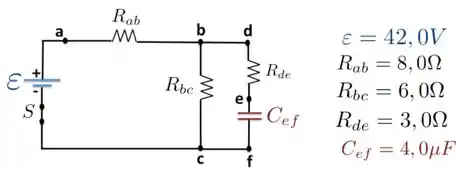
O circuito indicado na figura abaixo mostra um capacitor que está inicialmente descarregado. A chave está fechada no instante . Sobre essa situação,
- Qual é a corrente que passa através de cada resistor imediatamente após a chave ser fechada?
- Qual é a corrente que passa através de cada resistor imediatamente no instante de tempo ?
- Qual é a carga final do sobre o capacitor?
Passo 1
a) Qual é a corrente que passa através de cada resistor imediatamente após a chave ser fechada?
Mostramos na teoria para você que se o capacitor está descarregado em , então ele não tem carga nenhuma
Bom, se não tem carga alguma no capacitor, isso significa que a diferença de potencial entre as placas também é zero, porque:
No entanto, porém, todavia, como a corrente é diferente de zero através do capacitor, , passa uma corrente também através do resistor , que está em série com o capacitor. Para , então, como , podemos simplicar o circuito da figura acima para o seguinte:
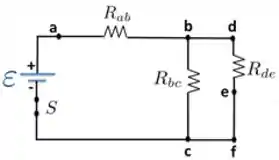
Passo 2
Analisando esse novo circuito que redesenhamos, podemos ver que há uma associação de resistores, sendo que e estão em paralelo e o resultado dessa associação está em série com o resistor .
Primeiro vamos calcular a resistência equivalente, , para associação em paralelo de e :
Agora, vamos calcular a nossa resistência equivalente total, , da associação em paralelo de e :
Então a resistência equivalente nesse caso será:
Onde:
Então:
A corrente do circuito é dada por:
Então, a corrente é, então:
Passo 3
b) Qual é a corrente que passa através de cada resistor imediatamente no instante de tempo ?
Para o tempo fica ainda mais simples o circuito!! Duvida?? Então segue...
Para um tempo muito grande, ou seja, , o capacitor fica totalmente carregado e nenhuma corrente flui mais através dele: . Então, também não passa nenhuma corrente pelo resistor que está em série com esse capacitor! Isso significa que podemos “jogar fora” (=”analisar o circuito como se o componente não existissem”) esse resistor e o capacitor na nossa análise e simplificar o circuito para:
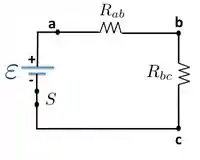
Agoa só temos uma associação em série dos resistores e . Então a resistência equivalente será:
Como:
Então:
Logo, a corrente será:
Passo 4
c) Qual é a carga final do sobre o capacitor?
Para um capacitor, temos a seguinte expressão:
A carga no capacitor é máxima quando , então a carga máxima será dada por:
Como nesse instante não passa corrente no trecho onde está o capacitor, ele está à mesma diferença de potencial que está o resistor .
Podemos escrever a diferença de potencial nesse ressitor como:
E como , podemos substituir essa expressão na expressão para a carga do capacitor:
Como:
Lembrando que temos que utilizar a corrente quando porqeu é nesse momento que a carga no capacitor é máxima.
Logo:
Se você entender bem este Exercício de fixação e outros parecidos que a gente resolve com você aqui, vai conseguir matar um monte de problemas desse tipo, vai por mim... ;-)