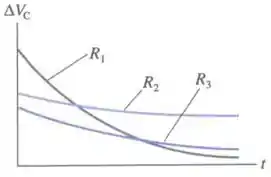
A figura abaixo mostra a voltagem em função do tempo de um capacitor enquanto ele é descarregado (separadamente) através de três diferentes resistores. Qual a alternativa que melhor descreve a relação entre a resistência destes três resistores?
(a)
(b)
(c) .
(d)
(e)
Passo 1
Aqui, vamos olhar para a constante de tempo capacitiva, dada por Ela nos diz sobre a velocidade de decaimento da tensão no capacitor da seguinte forma: quanto maior for , mais lentamente a tensão tenderá a zero.
Percebemos, pelo gráfico, que . Como a capacitância é a mesma para as três curvas, a relação entre as resistências será:
Resposta
(a)
Exercícios de Livros Relacionados
O capacitor C da Figura 25-49 está inicialmente descarregado. Logo após o interruptor S ser fechado, (a) a tensão em C é igual a E, (b) a tensão em R é E. (c) a corrente no circuito é zero, (d) ambas
O circuito mostrado na figura abaixo é uma ponte de Wheatstone e o resistor variável está sendo usado como um potenciômetro de fio deslizante. A resistência R 0 é conhecida. Esta “ponte” PE usada para
Mostre que a Equação d Q d t = ℇ C - Q R C ℇ pode ser reescrita como d Q ℇ C - Q = d t R C ℇ . Integre esta equação para derivar a solução dada pela Equação Q f ( 1 - e - t / R C ) .
No circuito mostrado na figura abaixo, o capacitor tem capacitância de 2.50 μ F e o resistor tem resistência de 0.500M Ω . Antes de a chave ser fechada, a queda de potencial no capacitor é 12.0V , com
A Fig. 27-67 mostra dois circuitos com um capacitar carregado que pode ser descarregado através de um resistor quando uma chave é fechada. Na Fig. 27-67a, R 1 = 20,0 Ω e C 1 = 5,00 μ F . Na Fig. 27-67