A vida útil de determinadas baterias termina quando elas fornecem toda a energia interna capaz de manter a sua . Considere uma bateria de e com capacidade de energia de . Suponha que a bateria seja ideal (sem resistência interna). Com esta bateria no circuito da Figura 1, onde , determine:
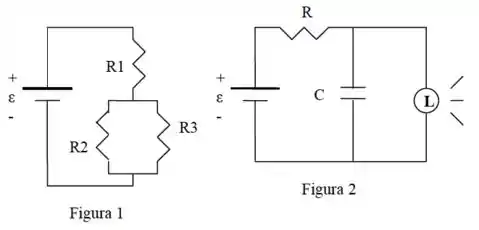
A potência fornecida pela bateria.
A vida útil neste circuito expressa em horas.
Uma nova bateria do mesmo tipo que a anterior é utilizada no circuito da Figura 2, onde e . Trata-se de um circuito de emissão repetitiva de “flashes” de luz. Quando a voltagem do capacitor atinge 2/3 do seu valor máximo, a lâmpada emite um “flash” de luz e descarrega-o instantaneamente, repetindo-se o ciclo.
O intervalo de tempo (período) entre “flashes”.
A quantidade de “flashes” emitidos durante a vida útil da bateria.
Em cada ciclo, a razão entre a energia armazenada em e a dissipada em .
Passo 1
A potência fornecida pela bateria.
Tem umas fórmulas manjadas para calcular a potência que já te perseguem desde o ensino médio.
Qualquer uma delas vai resolver a nossa vida. Mas como o problema já nos deu a e as resistências, é mais jogo aqui calcularmos a resistência equivalente e usarmos a segunda dessas fórmulas que eu coloquei ali em cima.
Passo 2
Pra calcular a resistência equivalente, vamos começar pelos dois resistores em paralelo.
Como .
Agora podemos calcular a resistência equivalente do circuito:
Onde .
Finalmente, agora podemos calcular a potência fornecida pela bateria.
Passo 3
A vida útil neste circuito expressa em horas.
O problema nos disse que a vida útil é o tempo necessário pra bateria gastar toda a sua energia... a energia da bateria aqui vale .
Usando a definição de potência:
Passo 4
O intervalo de tempo (período) entre “flashes”.
Em um circuito , a voltagem no capacitor obedece a seguinte equação:
Onde é a constante de tempo capacitiva, dada por:
Logo:
O problema falou que um flash é emitido quando o capacitor atinge 2/3 do seu valor máximo. Então precisamos descobrir quanto tempo levará para que um flash seja emitido.
O valor máximo da voltagem no capacitor é:
Logo:
Passo 5
A quantidade de “flashes” emitidos durante a vida útil da bateria.
O segredo aqui é encontrarmos a energia dissipada a cada “flash”... assim vamos poder descobrir quantos ”flashes” serão emitidos.
A energia, por definição, pode ser escrita como:
Nesse caso, vamos escrever a potência como já que, para esse caso, já sabemos que a corrente no capacitor é dada por:
Agora sim! Como queremos saber a energia dissipada em um “flash” e sabemos que o tempo para que seja disparado um “flash” é de , vamos integrar a potência entre 0 e 1,1.
Pra sabermos o número de flash, temos apenas que calcular:
Passo 6
Em cada ciclo, a razão entre a energia armazenada em e a dissipada em .
- Capacitor:
- Resistor:
A energia armazenada no capacitor é dada por:
Em um ciclo, a voltagem no capacitor é igual a 2/3 da voltagem máxima, logo?
Logo:
No passo anterior, calculamos a energia dissipada em um flash... parte dessa energia é armazenada pelo capacitor e a outra parte será dissipada pelo resistor.
Logo:
Assim, a razão é dada por:
Resposta