Considere um circuito elétrico constituído por uma bateria ideal de fem , duas resistências e e um capacitor de capacitância , conforme a figura a seguir.
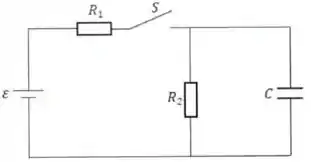
O circuito encontra-se inicialmente aberto (chave S aberta), com o capacitor totalmente descarregado. A chave S é então fechada e após um longo tempo, o capacitor acumula uma carga de . Quanto vale a fem da bateria?
Passo 1
Quando o problema diz que a chave ficou fechada por um longo tempo, como o capacitor está conectado à bateria, vamos considera-lo totalmente carregado.
Como o capacitor está em paralelo com o resistor , a ddp através de ambos é a mesma. Dessa forma, a corrente em será dada por:
Substituindo os valores:
Passo 2
Com o capacitor totalmente carregado a corrente através do mesmo torna-se nula. Dessa forma o circuito passa a ser constituído basicamente pela fem e pelos resistores e , associados em série.
Nessa configuração, como os resistores estão em série
Dessa forma, a fem será dada por:
Substituindo os valores:
Resposta