Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuito RC

Ver Teoria
Exercício 78123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767779808182

Enunciado

No circuito da figura abaixo:

  1. Determine as correntes em cada ramo.
  2. Calcule a diferença de potencial entre os pontos c e d .
  3. Calcule a potência fornecida por cada bateria.

Considere ε 1 = 5,0   V , ε 2 = 10 , 0   V , R 1 = 15,0 Ω , R 2 = 30,0 Ω e R 3 = 5,0 Ω .

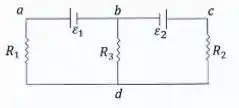
Passo 1

L e t r a   A :

Cara, uma das formas de encontrar as correntes em todos os ramos desse circuito é utilizando a Lei das Malhas de Kirchhoff, no qual a gente pega as duas malhas que temos aí e aplicamos correntes circulando em cada uma delas...

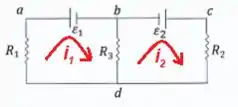
E agora, a gente coloca os sinais de + e - sobre todos os elementos de circuito para facilitar a análise: Lembre-se que o lado onde acorrente passa no resistor é positivo. As baterias ε tem lado positivo o lado maior...

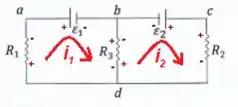
Agora, meu querido, é só aplicar o método nas duas malhas, lembrando que onde a corrente entra você considera aquele sinal. No caso de R 3 , como tem duas correntes, você tem que desconsiderar na equação:

1 ª   M a l h a :               + R 1 i 1 + ε 1 + R 3 + i 1 - i 2 = 0

2 ª   M a l h a :               R 3 + i 2 - i 1 - ε 2 + R 2 i 2 = 0

Veja que o problema nos deu todo mundo nessas equações com exceção das correntes (é o que queremos): Considere ε 1 = 5,0   V , ε 2 = 10,0   V , R 1 = 15,0 Ω , R 2 = 30,0 Ω e R 3 = 5,0 Ω .

1 ª   M a l h a :                             15 i 1 + 5 + 5 i 1 - i 2 = 0

2 ª   M a l h a :               5 + i 2 - i 1 - 10 + 30 i 2 = 0

Então agora é só resolvermos o sistema e obtermos as duas correntes!

Passo 2

Para resolver esse sistema, podemos primeiro simplificar um pouco mais...

15 i 1 + 5 + 5 i 1 - i 2 = 0 5 + i 2 - i 1 - 10 + 30 i 2 = 0     →

15 i 1 + 5 + 5 i 1 - 5 i 2 = 0 5 i 2 - 5 i 1 - 10 + 30 i 2 = 0     →

20 i 1 - 5 i 2 = - 5 - 5 i 1 + 3 5 i 2 = 10     →

POW! Multiplicando a equação de baixo por 4 ...

20 i 1 - 5 i 2 = - 5 - 20 i 1 + 140 i 2 = 40     →

Somando a equação de cima com a de baixo...

20 i 1 - 20 i 1 - 5 i 2 + 140 i 2 = - 5 + 40     →

135 i 2 = 35     →

i 2 = 35 135     →

i 2 = 7 27 A

POW! Substituindo esse resultado então em uma das equações que tem i 1 ...

- 5 i 1 + 35 i 2 = 10   →

- 5 i 1 + 35 7 27 = 10     →

- 5 i 1 = 10 - 245 27   →

- 5 i 1 = 10 - 245 27   →

- 5 i 1 = 270 27 - 245 27   →

- 5 i 1 = 25 27 →

i 1 = - 5 27 A

Esse menos aí significa apenas que a corrente i 1 está indo na direção contrária que a que escolhemos, isto é...

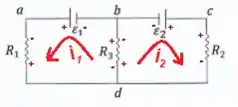
Passo 3

Então olha que maneiro, com essa brincadeira, a gente já determinou 2 das 3 correntes pedidas, afinal, ele pediu as correntes nos três ramos, e a corrente no ramo 1 e no ramo 2 ...

i 1 = 5 27 A               e               i 2 = 7 27 A

OBS: Veja que agora já estamos considerando a corrente i 1 positiva, já que estamos girando no sentido correto agora.

Para obter a terceira corrente é bem tranquilo! Observe que as duas correntes se juntam no nó d formando a corrente i 3 que passa pelo resistor R 3 :

i 3 = i 1 + i 2     →

i 3 = 5 27 + 7 27   →

i 3 = 12 27   A

Passo 4

L e t r a   B :

Cara, a diferença de potencial entre os pontos c e d pode ser calculada observando que só tem o resistor R 2 nesse caminho...

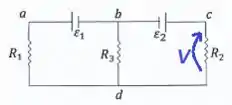
Portanto a diferença de potencial entre os pontos c   e d será igual a tensão em cima do resistor R 2 :

V c d = V

E pela Lei de Ohm...

V c d = R 2 i 2   →

V c d = 30 ⋅ 7 27   →

V c d = 10 ⋅ 7 9   →

V c d = 70 9 V

Passo 5

L e t r a   C :

Cara, a potência fornecida por cada Bateria vai ser...

p 1 = ε 1 i 1         p a r a   a   f o n t e   1

p 2 = ε 2 i 2         p a r a   a   f o n t e   2

Logo...

p 1 = 5 5 27 = 25 27   W

p 2 = 10 7 27 = 70 27   W

Resposta

Letra A:

i 1 = 5 27 A ;           i 2 = 7 27   A ;           i 3 = 12 27     A

Letra B:

V c d = 70 9 V

Letra C:

p 1 = 25 27 W         e           p 2 = 70 27 W

Exercícios de Livros Relacionados

O capacitor C da Figura 25-49 está inicialmente descarregado. Logo após o interruptor S ser fechado, (a) a tensão em C é igual a E, (b) a tensão em R é E. (c) a corrente no circuito é zero, (d) ambas
O circuito mostrado na figura abaixo é uma ponte de Wheatstone e o resistor variável está sendo usado como um potenciômetro de fio deslizante. A resistência R 0 é conhecida. Esta “ponte” PE usada para
Mostre que a Equação d Q d t = ℇ C - Q R C ℇ pode ser reescrita como d Q ℇ C - Q = d t R C ℇ . Integre esta equação para derivar a solução dada pela Equação Q f ( 1 - e - t / R C ) .
No circuito mostrado na figura abaixo, o capacitor tem capacitância de 2.50 μ F e o resistor tem resistência de 0.500M Ω . Antes de a chave ser fechada, a queda de potencial no capacitor é 12.0V , com
A Fig. 27-67 mostra dois circuitos com um capacitar carregado que pode ser descarregado através de um resistor quando uma chave é fechada. Na Fig. 27-67a, R 1 = 20,0 Ω e C 1 = 5,00 μ F . Na Fig. 27-67