No circuito indicado na figura abaixo, os capacitores estão inicialmente descarregados, a bateria não possui resistência interna e o amperímetro é ideal. Ache a leitura do amperímetro:
- Logo após a chave S ser fechada;
- Após a chave estar fechada há muito tempo.
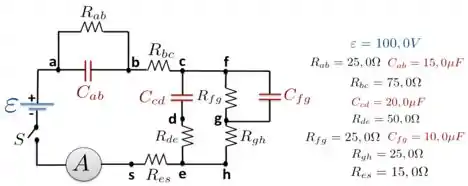
Passo 1
Você deve estar olhando para essa figura e se perguntando: “Pô, perae, você acabou de me mostrar uma teoria de um circuito RC simplizinho de uma malha, que eu consegui entender, e agora me vem com esse exercício com um monte de malhas, com um monte de resistores e capacitores distribuídos na maior loucura...deve tá de brincadeira comigo, né?”
CALMA, muita calma nessa hora...kkk Vou te mostrar que esse problema se reduz a um problema de associação de resistores em série e em paralelo...Duvida? Continua sem desanimar, que você vai ver...
Antes, quero discutir algumas coisas rápidas aqui com você. Olha só, você viu que se o capacitor está descarregado em , então ele não tem carga nenhuma: . Bom, se não tem carga alguma no capacitor, isso significa que a diferença de potencial entre as suas placas é
Por outro lado, para um tempo muito grande, ou seja, , o capacitor fica totalmente carregado e nenhuma corrente flui mais através dele: . Quase lá, quase... Essas duas características que comentei são FUNDAMENTAIS para você mater esse exercício...Dá uma olhada nelas de novo antes de seguir pro próximo passo!!
Passo 2
a) Agora, vamos colocar essas informações dos capacitores para lá no circuito da figura. Então, olha só, o potencial entre os pontos e da figura é . Isso significa que nenhuma corrente passa no resistor que está em paralelo a esse capacitor entre os pontos e , que é , mas passa corrente pelo capacitor . Por isso, podemos “eliminar esse resistor” do circuito para .
Podemos dizer o mesmo do resistor entre os pontos e , , que está em paralelo a outro capacitor. Bom, eliminamos, SEM NENHUMA CONTA, os resistores e ! \0/ \0/
CUIDADO: o resistor não pode ser eliminado, pois está em série com o capacitor e por esse capacitor passa uma corrente. FICA DE OLHO...
Como , nosso circuito da figura pode ser simplificado para:
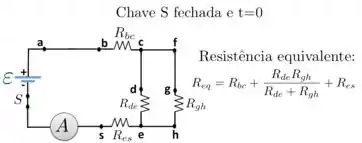
Então, o resistor está em paralelo com o resistor e o resistor equivalente dessa associação, que é
() está em série com os resistores e . A resistência total equivalente fica como
A corrente é
Passo 3
b) E agora para ? Bom, para esse caso, não passa nenhuma corrente pelos capacitores, então não passa corrente pelo trecho do circuito entre os pontos e da figura. Isso significa que podemos “eliminar esse trecho do circuito” para analisar a corrente e também desconsiderar em nossa análise os outros capacitores também.
Sobra o quê, então? Resta o seguinte circuito bem mais simples:
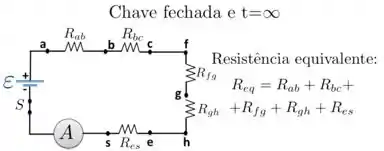
Advinha o que vamos usar agora para saber qual a resistência equivalente? Associação de resistores em série, que nesse caso:
Feliz ou não??
Agora, para fechar, a corrente para é
Fica atento, porque esse tipo análise de circuitos para os instantes e cai com bastante frequência nas provas…Fica de olho ;-) e pratica…