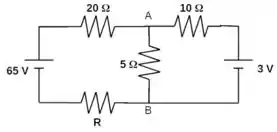
4ª questão - No circuito a seguir, um voltímetro verificou que há uma queda de potencial elétrico entre os pontos e (com ) igual a . Determine o valor da resistência .
A)
B)
C)
D)
E)
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎

Nessa questão, temos um circuito puramente resistivo como dado na figura do enunciado. Acontece que temos informações de todos os resistores, exceto um deles que chamamos de .
Então para obter o valor dessa resistência, tivemos a ideia de medir a tensão no ponto e a tensão no ponto do circuito. Dessa forma, vemos que a diferença de tensão do ponto para é de .
Com essas informações, temos que descobrir o valor de .
E aí, como podemos fazer isso?? 🤔🤔
Podemos usar o método da análise de malhas para descobrir a corrente que flui na malha da esquerda.
Bora dar uma olhada? 😁
Passo 2
Nesse método, a soma das tensões de cada componente em uma malha é igual a tensão da fonte de tensão, ou seja.
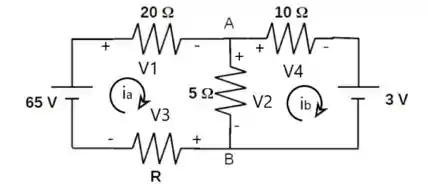
Para a malha da esquerda, vamos ter a seguinte equação
Para a malha da direita, percorrendo ela no sentido horário (logo, fonte de tensão negativa), temos:
Mas o que é , , e ? Pela lei de Ohm, a tensão é igual a corrente multiplicada pela resistência, ou seja
Já sabemos que é igual , portanto é igual a
Substituindo esses valores na malha da direita, temos
Logo, vemos que é
Tranquilo até aqui? 😉
Passo 3
Se , logo
Substituindo esses resultados na equação da malha da esquerda, temos
Resolvendo essa equação, vemos que
Com isso encontramos que
Analisando as alternativas, vemos que a alternativa A) corresponde a nossa resposta!
Fim! Iae, o que achou? Responde Aí! 😁

Resposta
A)