Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuito RC

Ver Teoria
Exercício 51234678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182

Enunciado

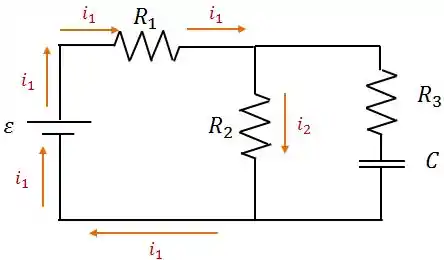
No circuito abaixo, ε = 1,2   kV , C = 6,5   μF , R 1 = R 2 = R 3 = 0,73   M Ω .

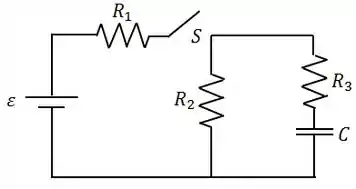
Com o capacitor C completamente descarregado, a chave S é fechada bruscamente no instante t = 0 .

Determine, para o instante t = 0 :

  1. A corrente i 1 no resistor 1;
  2. A corrente i 2 no resistor 2;
  3. A corrente i 3 no resistor 3;

    4. Determine, para t → ∞ (ou seja, após várias constantes de tempo):

  4. i 1 ;
  5. i 2 ;
  6. i 3 ;

    7. Determine a diferença de potencial V 2 no resistor 2:

  7. Em t = 0 ;
  8. Em t → ∞   ;
  9. Faça um esboço do gráfico de V 2 em função do tempo t no intervalo entre esses dois instantes extremos;

Passo 1

  1. Determine, para o instante t = 0 a corrente i 1 no resistor 1;

    2. O que a gente tem que atentar aqui é que a voltagem em um capacitor é dada pela seguinte expressão:

    V = q C

    Em t = 0 o capacitor está descarregado, ou seja, q = 0 e pela fórmula, a diferença de potencial no capacitor também será nula. Assim, nesse momento é como se o capacitor não existisse:

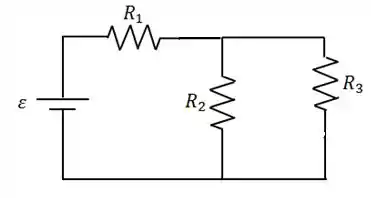
    Passo 2

    Agora, nós temos a seguinte situação no circuito:

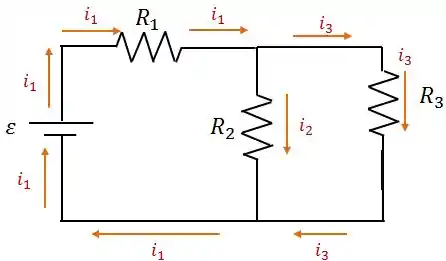
    Note que podemos dividir o circuito em duas malhas:

  • Malha 1: Resistores R 1 e R 2
  • Malha 2: Resistores R 1 e R 3

Vamos aplicar a Lei das Malhas para cada uma das malhas:

Malha 1:

ε - i 1 R 1 - i 2 R 2 = 0

Malha 2:

ε - i 1 R 1 - i 3 R 3 = 0

Temos duas equações, mas três variáveis ( i 1 , i 2 e i 3 ), então para resolver precisamos de mais uma equaçãozinha.

Vamos utilizar a Regra dos Nós, que nos diz que:

i 1 = i 2 + i 3

Então:

i 3 = i 1 - i 2

Se substituirmos a expressão para i 3 na Lei das malhas para a Malha 2 teremos um sisteminha de duas equações:

ε - i 1 R 1 - i 2 R 2 = 0

ε - i 1 R 1 - i 1 - i 2 R 3 = 0

Passo 2

Bora resolver esse sisteminha!!

ε - i 1 R 1 - i 2 R 2 = 0

ε - i 1 R 1 - i 1 - i 2 R 3 = 0

Onde:

ε = 1,2   kV = 1,2 × 10 3   V ;

R 1 = R 2 = R 3 = 0,73   M Ω = 7,3 × 10 5   Ω ;

Logo:

1,2 × 10 3 - 7,3 × 10 5   i 1 - 7,3 × 10 5   i 2 = 0

1,2 × 10 3 - 14,6 × 10 5   i 1 + 7,3 × 10 5   i 2 = 0  

Somando as duas equações:

2,4 × 10 3 - 21,9 × 10 5   i 1 = 0

i 1 = 2,4 × 10 3 21,9 × 10 5

i 1 = 1,1 × 10 - 3  A = 1,1  mA

Passo 3

  • Determine, para o instante t = 0 a corrente i 2 no resistor 2;

    • Para descobrir o valor de i 2 é só utilizar uma das equações do nosso sisteminha:

    Vamos usar essa

    ε - i 1 R 1 - i 2 R 2 = 0

    Onde:

    i 1 = 1,1   × 10 - 3   A ;

    Que encontramos anteriormente

    A nossa única incógnita é i 2 :

    1,2 × 10 3 - 7,3 × 10 5   .     1,1 × 10 - 3 - 7,3 × 10 5   i 2 = 0

    Logo:

    i 2 = 5,5   × 10 - 4  A = 0,55  mA  

    Passo 4

  • Determine, para o instante t = 0 a corrente i 3 no resistor 3;

    • Como já temos o valor de i 1 e i 2 , para achar i 3 vamos retornar para a Regra dos Nós:

    i 3 = i 1 - i 2

    Onde:

    i 1 = 1,1   m A ;

    i 2 = 0,55   m A ;

    Logo:

    i 3 = 0,5 5   m A

    Passo 5

  • Determine, para o instante t → ∞ a corrente i 1 no resistor 1;

    • Quando t → ∞ , o capacitor fica completamente carregado, portanto, a corrente deixa de correr no ramo onde ele está.

    Ou seja, i 3 = 0  

    Além disso, a corrente i 1 não se divide, pois só há um caminho para percorrer, então:

    i 1 = i 2

    Passo 6

    Vamos aplicar a Lei das malhas para essa nossa situação:

    ε - i 1 R 1 - i 2 R 2 = 0

    Como i 1 = i 2 e R 1 = R 2 , temos:

    ε - i 1 R 1 - i 1 R 1 = 0

    ε - 2   i 1 R 1 = 0

    ε = 2   i 1 R 1

    Então, i 1 será dada por:

    i 1 = ε 2 R 1 = 1,2.10 3 2 . 0,73.10 6 = 8,2   × 10 - 4   A = 0,82   m A

    Passo 7

  • Determine, para o instante t → ∞ a corrente i 2 no resistor 2;

    • Já vimos que i 1 = i 2 , então:

    i 2 = i 1 = 0,82   m A

    Passo 8

  • Determine, para o instante t → ∞ a corrente i 3 no resistor 3;

    • Já analisamos que nesse caso, nenhuma corrente passa pelo ramo do capacitor, então:

    i 3 = 0   A

    Passo 9

  • Determine a diferença de potencial V 2 no resistor 2 em t = 0 ;

    • Quando t = 0 a corrente que passa pelo resistor 2 é i 2 = 0,55   m A = 0,55 × 10 - 3 A . Logo:

    V 2 = R 2 i 2

    Onde R 2 = 0,73   M Ω = 0,73 × 10 6   Ω . Logo:

    V 2 = 0,73 × 10 6 × 0,55 × 10 - 3

    V 2 = 4,015 × 10 2   V = 401,5   V

    Passo 10

  • Determine a diferença de potencial V 2 no resistor 2 em t → ∞ ;

    • Quando t → ∞ , a corrente que passa pelo resistor 2 é i 2 = 0,82   m A = 0,82 × 10 - 3 A . Logo:

    V 2 = R 2 i 2

    V 2 = 0,73 × 10 6 × 0,82 × 10 - 3

    V 2 = 5,986   × 10 2 =   598,6   V

    Passo 11

  • Faça um esboço do gráfico de V 2 em função do tempo t no intervalo entre esses dois instantes extremos;

    • Vamos considerar agora a Malha 1 (que já identificamos no passo 2) e vamos definir uma Malha 3, formada pelo capacitor e pelos resistores 2 e 3.

    As equações das malhas serão:

    Malha 1:

    ε - i 1 R 1 - i 2 R 2 = 0

    Malha 3:

    - q C - i 3 R 3 + i 2 R 2 = 0

    Considerando que i 1 = i 2 + i 3 e que R 1 = R 2 = R 3 = R e substituindo isso na equação da Malha 1, teremos:

    ε - ( i 2 + i 3 ) R - i 2 R = ε - 2 i 2 R - i 3 R = 0

    i 2 = ( ε - i 3 R ) / 2 R

    Substituindo esse resultado na equação da Malha 3, temos:

    - q C - i 3 R + ε - i 3 R 2 R × R = 0

    - q C - i 3 R + ε 2 - i 3 R 2 = 0

    Sendo:

    i 3 = d q d t

    Temos:

    - q C - R d q d t + ε 2 - d q d t R 2 = 0

    3 R 2 d q d t + q C = ε 2

    Essa equação é semelhante àquela que vimos na teoria, com algumas pequenas diferenças. No nosso caso,

    τ = 3 R C 2

    E o potencial é:

      ε 2

    Logo, a solução dessa equação é:

    i 3 t = ε 3 R e - 2 t 3 R C

    Como vimos, a corrente i 2 será dada por:

    i 2 = ε - i 3 R 2 R

    Substituindo em i 2 a expressão que achamos para i 3 , temos:

    i 2 = ε - ε 3 R e - 2 t 3 R C R 2 R = ε 2 R - ε 6 R e - 2 t 3 R C

    Daí, temos:

    V 2 t = i 2 R = ε 2 R - ε 6 R e - 2 t 3 R C R =   ε 6 3 - e - 2 t 3 R C

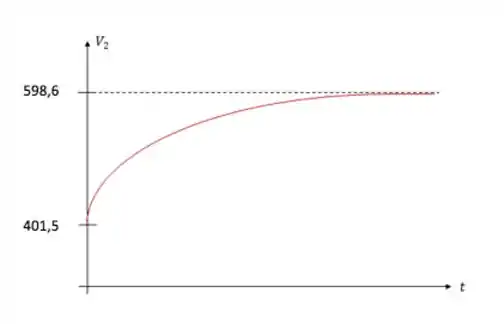
    Então o gráfico da diferença de potencial tem mais ou menos essa cara:

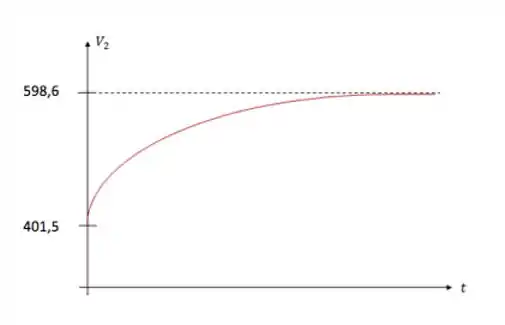
    Resposta

    1. i 1 = 1,1   mA ;
    2. i 2 = 0,55   m A ;
    3. i 3 = 0,55   m A ;
    4. i 1 = 0,82   m A ;
    5. i 2 = 0,82   m A ;
    6. i 3 = 0   A ;
    7. V 2 = 401,5   V ;
    8. V 2 = 598,6   V ;

    Exercícios de Livros Relacionados

    O capacitor C da Figura 25-49 está inicialmente descarregado. Logo após o interruptor S ser fechado, (a) a tensão em C é igual a E, (b) a tensão em R é E. (c) a corrente no circuito é zero, (d) ambas
    O circuito mostrado na figura abaixo é uma ponte de Wheatstone e o resistor variável está sendo usado como um potenciômetro de fio deslizante. A resistência R 0 é conhecida. Esta “ponte” PE usada para
    Mostre que a Equação d Q d t = ℇ C - Q R C ℇ pode ser reescrita como d Q ℇ C - Q = d t R C ℇ . Integre esta equação para derivar a solução dada pela Equação Q f ( 1 - e - t / R C ) .
    No circuito mostrado na figura abaixo, o capacitor tem capacitância de 2.50 μ F e o resistor tem resistência de 0.500M Ω . Antes de a chave ser fechada, a queda de potencial no capacitor é 12.0V , com
    A Fig. 27-67 mostra dois circuitos com um capacitar carregado que pode ser descarregado através de um resistor quando uma chave é fechada. Na Fig. 27-67a, R 1 = 20,0 Ω e C 1 = 5,00 μ F . Na Fig. 27-67