Um circuito é conectado a uma fonte de tensão por meio de uma chave que inicialmente está aberta. A chave é fechada em .
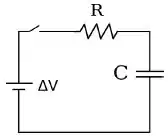
Considerando este circuito, qual das seguintes sentenças está CORRETA?
O capacitor fica completamente carregado no tempo 𝝉 e a corrente é nula neste instante.
A diferença de potencial através do resistor é sempre igual a do capacitor.
A diferença de potencial através do resistor é sempre maior que a do capacitor.
A diferença de potencial através do capacitor é sempre maior que a do resistor.
Quando o capacitor estiver completamente carregado, não haverá corrente elétrica no circuito.
Passo 1
Quando o capacitor está carregando, a carga no mesmo varia de acordo com a expressão abaixo:
Já a corrente no mesmo varia com o tempo de acordo com a expressão abaixo:
Passo 2
O capacitor fica completamente carregado no tempo 𝝉 e a corrente é nula neste instante.
Analisando a expressão da carga que vimos no passo 1:
Vemos que o capacitor fica totalmente carregado somente quando o tempo tende ao infinito, logo, essa afirmação é falsa.
Passo 3
As alternativas , e comparam a ddp através do capacitor com a ddp através do resistor. Vamos lá!
A ddp através do capacitor é dada por:
E a ddp através do resistor é dada por:
Repare que a ddp no capacitor é inicialmente nula e vai aumentando com o tempo, até que, para , o capacitor se carrega e .
Já no caso do resistor ocorre o contrário, a ddp é inicialmente , e vai decaindo com o tempo até que, para , . Dessa forma, nenhuma das três alternativas está correta.
Passo 4
Quando o capacitor estiver completamente carregado, não haverá corrente elétrica no circuito.
Como já falamos, o capacitor se carrega completamente em . De acordo com a equação da corrente, quanto , a corrente elétrica tende a zero.
Logo, a afirmativa está correta.
Resposta
Quando o capacitor estiver completamente carregado, não haverá corrente elétrica no circuito.