Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuito RC

Ver Teoria
Exercício 32123456789101112131415161718192021222324252627282930313334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182

Enunciado

Considere o circuito da figura abaixo e determine:

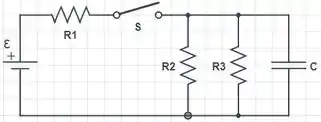
(a) a diferença de potencial através do capacitor após a chave S ter estado fechada por um tempo muito longo;

(b) a energia armazenada no capacitor depois de um tempo muito longo.

Depois que a chave é aberta, calcule:

(c) a corrente em função do tempo que atravessa o capacitor;

(d) a energia que é dissipada no resistor R 3 durante o processo de descarga do capacitor.

Passo 1

a)

Após um tempo muito longo, a corrente que circula por ele será nula, ou seja, i C = 0 .

Assim sendo, a corrente i 1 que circula pelo resistor R 1 será igual à soma das correntes i 2 e i 3 , que circulam pelos resistores R 2 e R 3 . Temos que:

i 1 = i 2 + i 3 .

Passo 2

Os resistores R 2 e R 3 estão em paralelo, a resistência equivalente entre esses dois caras vai ser

1 R e q 2 3 = 1 R 3 + 1 R 2

R e q 2 3 = R 3 R 2 R 3 + R 2

e essa resistência equivalente está em série com R 1 , logo a resistência equivalente total será

R e q = R 1 + R e q 2 3 = R 1 + R 3 R 2 R 3 + R 2

R e q = R 1 R 2 + R 1 R 3 + R 2 R 3 R 2 + R 3

Sabendo disso, podemos calcular a corrente i 1 como:

i 1 = ε R e q = ε R 1 R 2 + R 1 R 3 + R 2 R 3 R 2 + R 3

i 1 = ε R 2 + R 3 R 1 R 2 + R 1 R 3 + R 2 R 3

Passo 3

As tensões em R 2 e R 3 , V 2 e V 3 , são iguais, já que esses resistores estão em paralelo. Temos:

V 2 = V 3 → R 2 i 2 = R 3 i 3 ,

i 2 = R 3 R 2 i 3 .

Logo,

i 2 + i 3 = i 1

Substituindo i 2 e i 1

R 3 R 2 i 3 + i 3 = ε R 2 + R 3 R 1 R 2 + R 1 R 3 + R 2 R 3 ,

R 3 + R 2 R 2 i 3 = ε R 2 + R 3 R 1 R 2 + R 1 R 3 + R 2 R 3 ,

i 3 = ε R 2 R 1 R 2 + R 1 R 3 + R 2 R 3 .

Passo 4

Por fim, a tensão V C no capacitor é igual à tensão em V 3 . Temos:

V C = R 3 i 3 ,

V C = R 2 R 3 R 1 R 2 + R 1 R 3 + R 2 R 3 ε .

Passo 5

b)

A energia armazenada no capacitor é dada por:

U = 1 2 C V C 2 = 1 2 C ε 2 R 2 R 3 R 1 R 2 + R 1 R 3 + R 2 R 3 2 .

Passo 6

c)

Podemos redesenhar o circuito como a figura abaixo, onde

R 23 = R 2 R 3 R 2 + R 3 .

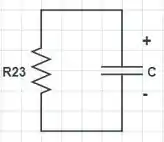
A corrente i t que circula no circuito é dada por i t = d q d t . Logo,

R 23 d q d t + q C = 0 .

Passo 7

A solução q ( t ) para a equação diferencial acima é dada por:

q t = q 0 e - t R 23 C   ,

com

q 0 = C V C = R 2 R 3 R 1 R 2 + R 1 R 3 + R 2 R 3 ε C .

Passo 8

Logo, a corrente i t será dada por:

i t = d q d t = i 0 e - t R 23 C   ,

com

i 0 = - R 2 + R 3 ε R 1 R 2 + R 1 R 3 + R 2 R 3 .

Passo 9

Durante a descarga, a energia inicial se dissipa nos resistores R 2 e R 3 , ou seja,

U = W 2 + W 3 .

Como a potência dissipada é proporcional ao inverso da resistência, ou seja, P = V 2 R , temos que:

P 2 P 3 = W 2 W 3 = R 3 R 2 .

Logo,

U = W 3 + W 3 R 3 R 2 = W 3 R 2 + R 3 R 2 .

Por fim,

W 3 = R 2 R 2 + R 3 U ,

W 3 = R 2 R 2 + R 3 1 2 C ε 2 R 2 R 3 R 1 R 2 + R 1 R 3 + R 2 R 3 2 ,

W 3 = 1 2 C ε 2 R 2 R 2 + R 3 R 2 R 3 R 1 R 2 + R 1 R 3 + R 2 R 3 2 .

Resposta

(a) V C = R 2 R 3 R 1 R 2 + R 1 R 3 + R 2 R 3 ε .

(b) U = 1 2 C ε 2 R 2 R 3 R 1 R 2 + R 1 R 3 + R 2 R 3 2 .

(c) i t = d q d t = i 0 e - t R 23 C , com i 0 = - R 2 + R 3 ε R 1 R 2 + R 1 R 3 + R 2 R 3 .

(d) W 3 = 1 2 C ε 2 R 2 R 2 + R 3 R 2 R 3 R 1 R 2 + R 1 R 3 + R 2 R 3 2 .

Exercícios de Livros Relacionados

O capacitor C da Figura 25-49 está inicialmente descarregado. Logo após o interruptor S ser fechado, (a) a tensão em C é igual a E, (b) a tensão em R é E. (c) a corrente no circuito é zero, (d) ambas
O circuito mostrado na figura abaixo é uma ponte de Wheatstone e o resistor variável está sendo usado como um potenciômetro de fio deslizante. A resistência R 0 é conhecida. Esta “ponte” PE usada para
Mostre que a Equação d Q d t = ℇ C - Q R C ℇ pode ser reescrita como d Q ℇ C - Q = d t R C ℇ . Integre esta equação para derivar a solução dada pela Equação Q f ( 1 - e - t / R C ) .
No circuito mostrado na figura abaixo, o capacitor tem capacitância de 2.50 μ F e o resistor tem resistência de 0.500M Ω . Antes de a chave ser fechada, a queda de potencial no capacitor é 12.0V , com
A Fig. 27-67 mostra dois circuitos com um capacitar carregado que pode ser descarregado através de um resistor quando uma chave é fechada. Na Fig. 27-67a, R 1 = 20,0 Ω e C 1 = 5,00 μ F . Na Fig. 27-67