UFJF – Física 3 – AV3 – 2018.2 – Questão 2c
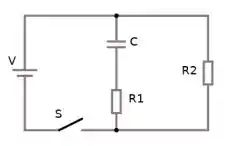
No circuito indicado na figura ao lado, o capacitor está inicialmente descarregado e o interruptor aberto. e são resistores. Em um instante inicial o interruptor é fechado.
c) Apresente a equação diferencial que rege a carga no capacitor em função do tempo, após o interruptor ser fechado.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um circuito com uma chave aberta. Com isso, ela nos pergunta qual é a equação diferencial que rege a carga no capacitor em função do tempo, após o interruptor ser fechado.
Para isso, temos que ter em mente a Lei de Ohm:
Onde é a tensão, é a resistência e é a corrente.
Uma boa ideia é aplicar a Lei de Kirchhoff das Tensões (LKT) a fim de observar o comportamento do circuito.
E aí? Bora responder?
Passo 2
Bom... aplicando LKT na malha esquerda do circuito, temos:
Onde é a tensão na fonte, é a tensão no capacitor e é a tensão em .
Lembrando que:
Onde é a carga do capacitor e é sua capacitância.
Além disso, temos também que
Em que é a corrente em função da carga do capacitor.
Passo 3
Assim, substituindo em
Temos que:
Entendeu direitinho? Responde aee ;)
